
 x2+10x;A产品年产量大于80万件时,C(x)=51x+
x2+10x;A产品年产量大于80万件时,C(x)=51x+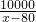 -1450.因设备限制,A产品年产量不超过200万件.现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完.设该厂生产A产品的年利润为L(万元).
-1450.因设备限制,A产品年产量不超过200万件.现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完.设该厂生产A产品的年利润为L(万元).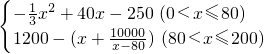 ;
;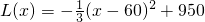 ,所以
,所以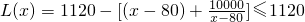
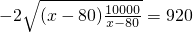 .
.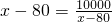 ,即x=180时,“=”成立.
,即x=180时,“=”成立.

科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
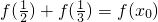 ,求x0的值;
,求x0的值;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
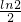 ,
, ,c=
,c=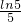 ,则
,则查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 在(0,+∞)上都是减函数,则函数f(x)=bx+a在R上是
在(0,+∞)上都是减函数,则函数f(x)=bx+a在R上是查看答案和解析>>
科目:高中数学 来源: 题型:填空题
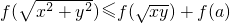 恒成立,则实数a的取值范围是________.
恒成立,则实数a的取值范围是________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com