
【题目】(本小题满分12分,(1)小问7分,(2)小问5分)
设函数![]()
(1)若![]() 在
在![]() 处取得极值,确定
处取得极值,确定![]() 的值,并求此时曲线
的值,并求此时曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 在
在![]() 上为减函数,求
上为减函数,求![]() 的取值范围。
的取值范围。
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】某科研机构研发了某种高新科技产品,现已进入实验阶段.已知实验的启动资金为10万元,从实验的第一天起连续实验,第![]() 天的实验需投入实验费用为
天的实验需投入实验费用为![]() 元
元![]() ,实验30天共投入实验费用17700元.
,实验30天共投入实验费用17700元.
(1)求![]() 的值及平均每天耗资最少时实验的天数;
的值及平均每天耗资最少时实验的天数;
(2)现有某知名企业对该项实验进行赞助,实验![]() 天共赞助
天共赞助![]() 元
元![]() .为了保证产品质量,至少需进行50天实验,若要求在平均每天实际耗资最小时结束实验,求
.为了保证产品质量,至少需进行50天实验,若要求在平均每天实际耗资最小时结束实验,求![]() 的取值范围.(实际耗资=启动资金+试验费用-赞助费)
的取值范围.(实际耗资=启动资金+试验费用-赞助费)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取40名中学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段: ![]() ,
, ![]() ,…,
,…, ![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
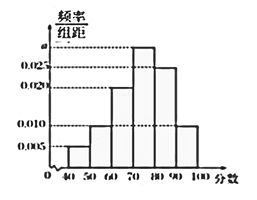
(1)求图中实数![]() 的值;
的值;
(2)若该校高一年级共有640人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在![]() 与
与![]() 两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与y轴的正半轴相交于点M,且椭圆E上相异两点A、B满足直线MA,MB的斜率之积为
与y轴的正半轴相交于点M,且椭圆E上相异两点A、B满足直线MA,MB的斜率之积为![]() .
.
(Ⅰ)证明直线AB恒过定点,并求定点的坐标;
(Ⅱ)求三角形ABM的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(Ⅰ)求曲线![]() 的直角坐标方程,并指出其表示何种曲线;
的直角坐标方程,并指出其表示何种曲线;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若点
两点,若点![]() 的直角坐标为
的直角坐标为![]() ,
,
试求当![]() 时,
时, ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=![]() ,DE=3,∠BAD=60,G为BC的中点.
,DE=3,∠BAD=60,G为BC的中点.
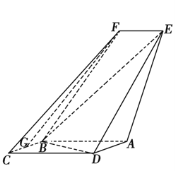
(1)求证:FG![]() 平面BED;
平面BED;
(2)求证:平面BED⊥平面AED;
(3)求直线EF与平面BED所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com