
| A. | $\frac{5}{204}$ | B. | $\frac{45}{68}$ | C. | $\frac{15}{68}$ | D. | $\frac{5}{68}$ |
分析 基本事件总数n=${C}_{18}^{3}$,3人来自不同学习小组包含的基本事件个数m=${C}_{6}^{3}$,由此能求出3人来自不同学习小组的概率.
解答 解:六个学习小组依次编号为1、2、3、4、5、6,每组3人,
现需从中任选3人组成一个新的学习小组,
基本事件总数n=${C}_{18}^{3}$,
3人来自不同学习小组包含的基本事件个数m=${C}_{6}^{3}$,
∴3人来自不同学习小组的概率为p=$\frac{m}{n}$=$\frac{{C}_{6}^{3}}{{C}_{18}^{3}}$=$\frac{5}{204}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
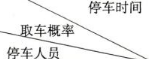 | (0,2] | (2,3] | (3,4] | (4,5] |
| 甲 | $\frac{1}{2}$ | x | x | x |
| 乙 | $\frac{1}{6}$ | $\frac{1}{3}$ | y | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{5}{7}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面为矩形,PA是四棱锥的高,AP=AB=2,F是PB的中点,E是BC上的动点.
如图,四棱锥P-ABCD的底面为矩形,PA是四棱锥的高,AP=AB=2,F是PB的中点,E是BC上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,⊙O与x轴的正半轴交点为A,点B,C在⊙O上,且B($\frac{4}{5}$,-$\frac{3}{5}$),点C在第一象限,∠AOC=α,BC=1,则cos($\frac{5π}{6}$-α)=( )
如图,⊙O与x轴的正半轴交点为A,点B,C在⊙O上,且B($\frac{4}{5}$,-$\frac{3}{5}$),点C在第一象限,∠AOC=α,BC=1,则cos($\frac{5π}{6}$-α)=( )| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最大值-2 | B. | 最小值-2 | C. | 最大值2$\sqrt{3}$ | D. | 最小值2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com