
【题目】定义在R上的奇函数![]() ,当
,当![]() 时,
时, 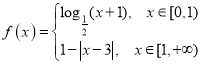
则函数![]() 的所有零点之和为_____.
的所有零点之和为_____.
【答案】![]()
【解析】
函数F(x)=f(x)﹣a(0<a<1)的零点转化为:在同一坐标系内y=f(x),y=a的图象交点的横坐标;作出两函数图象,考查交点个数,结合方程思想,及零点的对称性,根据奇函数f(x)在x≥0时的解析式,作出函数的图象,结合图象及其对称性,求出答案.
∵当x≥0时,
f(x)=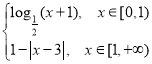
即x∈[0,1)时,f(x)=![]() (x+1)∈(﹣1,0];
(x+1)∈(﹣1,0];
x∈[1,3]时,f(x)=x﹣2∈[﹣1,1];
x∈(3,+∞)时,f(x)=4﹣x∈(﹣∞,﹣1);
画出x≥0时f(x)的图象,
再利用奇函数的对称性,画出x<0时f(x)的图象,如图所示;

则直线y=a,与y=f(x)的图象有5个交点,则方程f(x)﹣a=0共有五个实根,
最左边两根之和为﹣6,最右边两根之和为6,
∵x∈(﹣1,0)时,﹣x∈(0,1),
∴f(﹣x)=![]() (﹣x+1),
(﹣x+1),
又f(﹣x)=﹣f(x),
∴f(x)=﹣![]() (﹣x+1)=
(﹣x+1)=![]() (1﹣x)﹣1=log2(1﹣x),
(1﹣x)﹣1=log2(1﹣x),
∴中间的一个根满足log2(1﹣x)=a,即1﹣x=2a,
解得x=1﹣2a,
∴所有根的和为1﹣2a.
故答案为:1﹣2a.


科目:高中数学 来源: 题型:
【题目】设![]() ,下列命题:
,下列命题:
①![]() 既不是奇函数,也不是偶函数
既不是奇函数,也不是偶函数
②若![]() 是三角形的内角,则
是三角形的内角,则![]() 是增函数
是增函数
③若![]() 是三角形的内角, 则
是三角形的内角, 则![]() 有最大值而无最小值
有最大值而无最小值
④![]() 的最小正周期是
的最小正周期是![]()
其中真命题的序号是( )
A.①②B.①③C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,对于不相等的实数
,对于不相等的实数![]() 、
、![]() ,设
,设![]() ,
,![]() ,现有如下命题:
,现有如下命题:
①对于任意不相等的实数![]() 、
、![]() ,都有
,都有![]() ;
;
②对于任意的![]() 及任意不相等的实数
及任意不相等的实数![]() 、
、![]() ,都有
,都有![]() ;
;
③对于任意的![]() ,存在不相等的实数
,存在不相等的实数![]() 、
、![]() ,使得
,使得![]() ;
;
④对于任意的![]() ,存在不相等的实数
,存在不相等的实数![]() 、
、![]() ,使得
,使得![]() ;
;
其中所有的真命题的序号是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 y f(x) 的定义域为[2.1,2],其图像如下图所示,且 f(2.1) 0.96
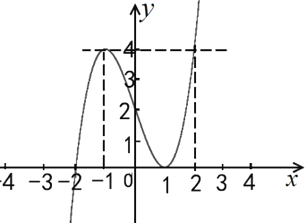
(1)若函数 yf(x) k恰有两个不同的零点,则 k_____
(2)已知函数 g ( x) ![]() , yg[f(x)] 有_____个不同的零点
, yg[f(x)] 有_____个不同的零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学经典名著,其中有这样一个问题:“今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有-圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该木材,锯口深一寸,锯道长-尺.问这块圆柱形木材的直径是多少?现有长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算该木材镶嵌在墙体中的体积约为__________立方寸.(结果保留整数)
寸,估算该木材镶嵌在墙体中的体积约为__________立方寸.(结果保留整数)
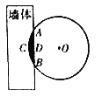
注:l丈=10尺=100寸,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com