
【题目】已知数列![]() 满足
满足![]() ,且
,且![]() .
.
(Ⅰ)证明:数列![]() 为等差数列,并求数列
为等差数列,并求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若记![]() 为满足不等式
为满足不等式![]() 的正整数
的正整数![]() 的个数,设
的个数,设![]() ,求数列
,求数列![]() 的最大项与最小项的值.
的最大项与最小项的值.
【答案】(1)见解析;(2)最大项为![]() ,最小项为
,最小项为![]() .
.
【解析】试题分析:(Ⅰ)对![]() 两边取倒数,移项即可得出
两边取倒数,移项即可得出![]() ,故而数列
,故而数列![]() 为等差数列,利用等差数列的通项公式求出
为等差数列,利用等差数列的通项公式求出![]() ,从而可得出
,从而可得出![]() ;(Ⅱ)根据不等式
;(Ⅱ)根据不等式![]() ,,得
,,得![]() ,又
,又![]() ,从而
,从而![]() ,当
,当![]() 为奇数时,
为奇数时,![]() 单调递减,
单调递减,![]() ;当
;当![]() 为偶数时
为偶数时![]() 单调递增,
单调递增,![]() 综上
综上![]() 的最大项为
的最大项为![]() ,最小项为
,最小项为![]() .
.
试题解析:(Ⅰ)由于![]() ,
,![]() ,则
,则![]()
∴![]() ,则
,则![]() ,即
,即![]() 为常数
为常数
又![]() ,∴数列
,∴数列![]() 是以1为首项,
是以1为首项,![]() 为公比的等比数列
为公比的等比数列
从而![]() ,即
,即![]() .
.
(Ⅱ)由![]() 即
即![]() ,得
,得![]() ,
,
又![]() ,从而
,从而![]()
故
当![]() 为奇数时,
为奇数时, ,
,![]() 单调递减,
单调递减,![]() ;
;
当![]() 为偶数时,
为偶数时, ,
,![]() 单调递增,
单调递增,![]()
综上![]() 的最大项为
的最大项为![]() ,最小项为
,最小项为![]() .
.
【题型】解答题
【结束】
22
【题目】已知向量![]() ,
,![]()
![]() ,若函数
,若函数![]() 的最小正周期为
的最小正周期为![]() ,且在区间
,且在区间![]() 上单调递减.
上单调递减.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)若关于![]() 的方程
的方程![]() 在
在![]() 有实数解,求
有实数解,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(Ⅰ)由平面向量数量积公式可得![]() ,利用二倍角的正弦公式、二倍角的余弦公式以及两角和与差的正弦公式将函数
,利用二倍角的正弦公式、二倍角的余弦公式以及两角和与差的正弦公式将函数![]() 化为
化为![]() ,利用正弦函数的周期公式可得
,利用正弦函数的周期公式可得![]() ,利用区间
,利用区间![]() 上单调递减,可得
上单调递减,可得![]() ,从而可得函数解析式;(Ⅱ)原方程可化为
,从而可得函数解析式;(Ⅱ)原方程可化为![]() 令
令![]() ,可得
,可得![]() ,整理
,整理![]() ,等价于
,等价于![]() 在
在![]() 有解,利用一元二次方程根的分布求解即可.
有解,利用一元二次方程根的分布求解即可.
试题解析:(Ⅰ)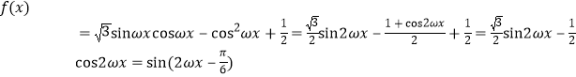
![]() ,∴
,∴![]()
当![]() 时,
时,![]() 此时
此时![]() 单增,不合题意,∴
单增,不合题意,∴![]() ;
;
∴![]() ,∴
,∴![]() ,在
,在![]() 单减,符合题意,故
单减,符合题意,故![]()
(Ⅱ)![]() ,
,![]() ,
,![]()
![]()
方程方程![]() 即为:
即为:
![]() 令
令![]() ,由
,由
![]() ,得
,得![]() ,于是
,于是![]()
原方程化为![]() ,整理
,整理![]() ,等价于
,等价于![]() 在
在![]() 有解
有解
解法一:
(1)当![]() 时,方程为
时,方程为![]() 得
得![]() ,故
,故![]() ;
;
(2)当![]() 时,
时,![]() 在
在![]() 上有解
上有解![]() 在
在![]() 上有解,问题转化为求函数
上有解,问题转化为求函数![]() 上的值域;设
上的值域;设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
设![]() ,在
,在![]() 时,单调递减,
时,单调递减,![]() 时,单调递增,∴
时,单调递增,∴![]() 的取值范围是
的取值范围是![]() ,
,
![]() 在
在![]() 上有实数解
上有实数解![]() 或
或![]()
解法二:记![]()
(1)当![]() 时,
时,![]() ,若
,若![]() 解得
解得![]() 不符合题意,所以
不符合题意,所以![]() ;
;
(2)当![]() ,方程
,方程![]() 在
在![]() 上有解;
上有解;
①方程在![]() 上恰有一解
上恰有一解![]() ;
;
②方程在![]() 上恰有两解
上恰有两解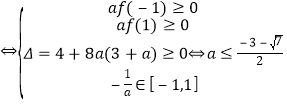 或
或![]() ;
;
综上所述,![]() 的范围是
的范围是![]() 或
或![]() .
.


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记![]() 为
为![]() OP所经过的在正方形ABCD内的区域(阴影部分)的面积
OP所经过的在正方形ABCD内的区域(阴影部分)的面积![]() ,那么对于函数
,那么对于函数![]() 有以下三个结论:
有以下三个结论:
①![]() ;
;
②任意![]() ,都有
,都有![]() ;
;
③任意![]() 且
且![]() ,都有
,都有![]() .
.
其中正确结论的序号是__________. (把所有正确结论的序号都填上).

【答案】①②
【解析】试题分析:①:如图,当![]() 时,
时, ![]() 与
与![]() 相交于点
相交于点![]() ,∵
,∵![]() ,则
,则![]() ,
,
∴![]() ,∴①正确;②:由于对称性,
,∴①正确;②:由于对称性, ![]() 恰好是正方形的面积,
恰好是正方形的面积,
∴![]() ,∴②正确;③:显然
,∴②正确;③:显然![]() 是增函数,∴
是增函数,∴![]() ,∴③错误.
,∴③错误.

考点:函数性质的运用.
【题型】填空题
【结束】
17
【题目】化简
(1)![]()
(2)![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax2﹣bx﹣1,其中a,b∈R,e=2.718 28…为自然对数的底数.
(1)设g(x)是函数f(x)的导函数,求函数g(x)在区间[0,1]上的最小值;
(2)若f(1)=0,函数f(x)在区间(0,1)内有零点,证明:e﹣2<a<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() )的最大值为
)的最大值为![]() ,最小值为
,最小值为![]() .
.
(1)求![]() 的值;
的值;
(2)将函数![]() 图象向右平移
图象向右平移![]() 个单位后,再将图象上所有点的纵坐标扩大到原来的
个单位后,再将图象上所有点的纵坐标扩大到原来的![]() 倍,横坐标不变,得到函数
倍,横坐标不变,得到函数![]() 的图象,求方程
的图象,求方程![]() 的解.
的解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP,E为棱PD中点. 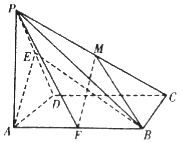
(1)求证:PD⊥平面ABE;
(2)若F为AB中点, ![]() ,试确定λ的值,使二面角P﹣FM﹣B的余弦值为-
,试确定λ的值,使二面角P﹣FM﹣B的余弦值为- ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的方程为 ![]() +
+ ![]() =1(a>b>0),双曲线
=1(a>b>0),双曲线 ![]() ﹣
﹣ ![]() =1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4
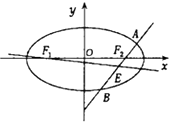
=1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4 ![]() .
.
(1)求椭圆C的方程;
(2)设F1 , F2分别为椭圆C的左,右焦点,过F2作直线l(与x轴不重合)交于椭圆于A,B两点,线段AB的中点为E,记直线F1E的斜率为k,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a>0且a≠1,函数f(x)=![]() x2-(a+1)x+alnx.
x2-(a+1)x+alnx.
(1)当a=2时,求曲线y=f(x)在(3,f(3))处切线的斜率;
(2)求函数f(x)的极值点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了解老人们的健康状况,政府从 老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能 自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行 统计,样本分布被制作成如图表: 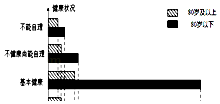
(1)若采取分层抽样的方法再从样本中的不能自理的老人中抽取16人进一步了解他们的生活状况,则两个群体中各应抽取多少人?
(2)估算该市80岁及以上长者占全市户籍人口的百分比;
(3)据统计该市大约有五分之一的户籍老人无固定收入,政府计划为这部分老人每月发 放生活补贴,标准如下:①80岁及以上长者每人每月发放生活补贴200元;②80岁以下 老人每人每月发放生活补贴120元;③不能自理的老人每人每月额外发放生活补贴100 元.试估计政府执行此计划的年度预算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com