
ЦцКЏЪ§
f(x)ЪЧЖЈвхдк(Ѓ¥ ЃЌЃЋ¥ )ЩЯЕФдіКЏЪ§ЃЌХМКЏЪ§g(x)дкЧјМф ЩЯЕФЭМЯёгыf(x)ЕФЭМЯёжиКЯЃЌЩшaЃОbЃО0ЃЌдкЯТСаВЛЕШЪНжае§ШЗЕФЪЧ
ЩЯЕФЭМЯёгыf(x)ЕФЭМЯёжиКЯЃЌЩшaЃОbЃО0ЃЌдкЯТСаВЛЕШЪНжае§ШЗЕФЪЧ
[
ЁЁЁЁ]Ђй
f(b)Ѓf(Ѓa)ЃОg(a)Ѓg(Ѓb)ЁЁЂкf(b)Ѓf(Ѓa)ЃМg(a)Ѓg(Ѓb)ЁЁЂлf(a)Ѓf(Ѓb)ЃОg(b)Ѓg(a)ЁЁЂмf(a)Ѓf(Ѓb)ЃМg(b)Ѓg(Ѓa)|
A ЃЎЂйЂм |
B ЃЎЂкЂл |
C ЃЎЂйЂл |
D ЃЎЂкЂм |

| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
вбжЊЦцКЏЪ§f(x)ЪЧЖЈвхдк(Ѓ3ЃЌ3)ЩЯЕФМѕКЏЪ§ЃЌЧвТњзуВЛЕШЪНf(xЃ3)+f(x2Ѓ3)<0,ЩшВЛЕШЪННтМЏЮЊAЃЌB=AЁШ{x|1ЁмxЁм![]() },ЧѓКЏЪ§g(x)=Ѓ3x2+3xЃ4(xЁЪB)ЕФзюДѓжЕЁЃ
},ЧѓКЏЪ§g(x)=Ѓ3x2+3xЃ4(xЁЪB)ЕФзюДѓжЕЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
вбжЊЦцКЏЪ§f(x)ЪЧЖЈвхдк(Ѓ3ЃЌ3)ЩЯЕФМѕКЏЪ§ЃЌЧвТњзуВЛЕШЪНf(xЃ3)+f(x2Ѓ3)<0,ЧѓxЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
вбжЊЦцКЏЪ§f(x)ЪЧЖЈвхдк(Ѓ3ЃЌ3)ЩЯЕФМѕКЏЪ§ЃЌЧвТњзуВЛЕШЪНf(xЃ3)+f(x2Ѓ3)<0,ЩшВЛЕШЪННтМЏЮЊAЃЌB=AЁШ{x|1ЁмxЁм![]() },ЧѓКЏЪ§g(x)=Ѓ3x2+3xЃ4(xЁЪB)ЕФзюДѓжЕ.
},ЧѓКЏЪ§g(x)=Ѓ3x2+3xЃ4(xЁЪB)ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК2010ФъКЃФЯЪЁИпЖўЯТбЇЦкЦкФЉВтЪдЪ§бЇЮФ ЬтаЭЃКбЁдёЬт
вбжЊЦцКЏЪ§f(x)ЪЧЖЈвхдкЃЈ-2ЃЌ2ЃЉЩЯЕФМѕКЏЪ§ЃЌШєf(m-1)+f(2m-1)>0ЃЌдђЪЕЪ§mЕФЗЖЮЇЪЧЃЈ ЃЉ
AЁЂ ЃМmЃМ
ЃМmЃМ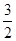 BЁЂ
BЁЂ ЃМmЃМ
ЃМmЃМ CЁЂ
CЁЂ ЃМmЃМ
ЃМmЃМ DЁЂ
DЁЂ ЃМmЃМ
ЃМmЃМ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
вбжЊЦцКЏЪ§f(x)ЪЧЖЈвхдк(-1ЃЌ1)ЩЯЕФМѕКЏЪ§ЃЌЧвf(1вЛt)+f(1-t2)<OЃЌЧѓtЕФжЕЗЖЮЇЁЃ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com