
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为菱形,且PA=PD=DA=2,∠BAD=60°
(I)求证:PB⊥AD;
(II)若PB=![]() , 求二面角A﹣PD﹣C的余弦值.
, 求二面角A﹣PD﹣C的余弦值.
【答案】
证明:(Ⅰ)取AD的中点E,连接PE,BE,BD.
∵PA=PD=DA,四边形ABCD为菱形,且∠BAD=60°,
∴△PAD和△ABD为两个全等的等边三角形,
则PE⊥AD,BE⊥AD,∴AD⊥平面PBE,
又PB平面PBE,∴PB⊥AD;
(Ⅱ)解:在△PBE中,由已知得,PE=BE=![]() ,PB=
,PB=![]() ,则PB2=PE2+BE2 ,
,则PB2=PE2+BE2 ,
∴∠PEB=90°,即PE⊥BE,又PE⊥AD,∴PE⊥平面ABCD;
以点E为坐标原点,分别以EA,EB,EP所在直线为x,y,z轴,建立如图所示空间直角坐标系,
则E(0,0,0),C(﹣2,![]() ,0),D(﹣1,0,0),P(0,0,
,0),D(﹣1,0,0),P(0,0,![]() ),
),
则![]() =(1,0,
=(1,0,![]() ),
),![]() =(﹣1,
=(﹣1,![]() ,0),
,0),
由题意可设平面APD的一个法向量为![]() =(0,1,0);
=(0,1,0);
设平面PDC的一个法向量为![]() =(x,y,z),
=(x,y,z),
由 得:![]() ,
,
令y=1,则x=![]() ,z=﹣1,∴
,z=﹣1,∴![]() =(
=(![]() ,1,﹣1);
,1,﹣1);
则![]()
![]() =1,∴cos<
=1,∴cos<![]() ,
,![]() >=
>=![]() =
=![]() =
=![]() ,
,
由题意知二面角A﹣PD﹣C的平面角为钝角,
所以,二面角A﹣PD﹣C的余弦值为﹣![]()

【解析】(Ⅰ)证明:取AD的中点E,连接PE,BE,BD.证明AD⊥平面PBE,然后证明PB⊥AD;
(Ⅱ)以点E为坐标原点,分别以EA,EB,EP所在直线为x,y,z轴,建立如图所示空间直角坐标系,求出平面APD的一个法向量为![]() =(0,1,0),平面PDC的一个法向量为
=(0,1,0),平面PDC的一个法向量为![]() , 利用向量的数量积求解二面角A﹣PD﹣C的余弦值.
, 利用向量的数量积求解二面角A﹣PD﹣C的余弦值.
【考点精析】解答此题的关键在于理解直线与平面垂直的性质的相关知识,掌握垂直于同一个平面的两条直线平行.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,弦CD⊥AB于点M,E是CD延长线上一点,AB=10,CD=8,3ED=4OM,EF切圆O于F,BF交CD于G. 
(1)求证:△EFG为等腰三角形;
(2)求线段MG的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,圆C的参数方程![]() (φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)直线l的极坐标方程是ρ(sinθ+![]() cosθ)=3
cosθ)=3![]() , 射线OM:θ=
, 射线OM:θ=![]() 与圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.
与圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于回归分析的说法中错误的有( )个
(1). 残差图中残差点所在的水平带状区域越宽,则回归方程的预报精确度越高.
(2). 回归直线一定过样本中心![]() 。
。
(3). 两个模型中残差平方和越小的模型拟合的效果越好。
(4) .甲、乙两个模型的![]() 分别约为0.88和0.80,则模型乙的拟合效果更好.
分别约为0.88和0.80,则模型乙的拟合效果更好.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二面角α﹣l﹣β为60°,ABα,AB⊥l,A为垂足,CDβ,C∈l,∠ACD=135°,则异面直线AB与CD所成角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
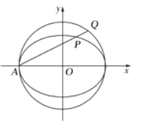
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,长轴长为4,过椭圆的左顶点
,长轴长为4,过椭圆的左顶点![]() 作直线
作直线![]() ,分别交椭圆和圆
,分别交椭圆和圆![]() 于相异两点
于相异两点![]()
(1) 若直线![]() 的斜率为1,求
的斜率为1,求![]() 的值:
的值:
(2) 若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com