
【题目】已知f(x)=2x2﹣3x+1,g(x)=ksin(x﹣ ![]() )(k≠0).
)(k≠0).
(1)设f(x)的定义域为[0,3],值域为A; g(x)的定义域为[0,3],值域为B,且AB,求实数k的取值范围.
(2)若方程f(sinx)+sinx﹣a=0在[0,2π)上恰有两个解,求实数a的取值范围.
【答案】
(1)解:当x∈[0,3]时,由于f(x)=2x2﹣3x+1图象的对称轴为 ![]() ,且开口向上,
,且开口向上,
可知 ![]() ,f(x)max=f(3)=10,
,f(x)max=f(3)=10,
所以f(x)的值域 ![]() ;
;
当x∈[0,3]时, ![]() ,
, ![]() ;所以当k>0时,g(x)的值域
;所以当k>0时,g(x)的值域 ![]() ;
;
所以当k<0时,g(x)的值域 ![]() ;
;
又∵AB,所以 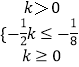 或
或 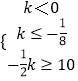 ;
;
即 k≥10或k≤﹣20;
(2)解:∵f(sinx)+sinx﹣a=0,所以2sin2x﹣2sinx+1﹣a=0在x∈[0,2π)上恰有两个解,
设t=sinx,则t∈[﹣1,1],令h(t)=2t2﹣2t+1﹣a,
①当t∈(﹣1,1)时,由题意h(t)=0恰有一个解或者有两个相等的解,
即h(﹣1)h(﹣1)<0或△=4﹣8(1﹣a)=0,即1<a<5或 ![]() ;
;
②若t=﹣1是方程2t2﹣2t+1﹣a=0的一个根,此时a=5,且方程的另一个根为t=2,于是sinx=﹣1或sinx=2,
因此 ![]() ,不符合题意,故a=5(舍);
,不符合题意,故a=5(舍);
③若t=1是方程2t2﹣2t+1﹣a=0的一个根,此时a=1,且方程的另一个根为t=0,于是sinx=1或sinx=0,
因此x=0或 ![]() 或π,不符合题意,故a=1(舍);
或π,不符合题意,故a=1(舍);
综上,a的取值范围是1<a<5或 ![]()
【解析】(1)根据二次函数和正弦函数的图象与性质,分别求出f(x)、g(x)在区间[0,3]上的最值即得值域A、B;再根据AB求出k的取值范围;(2)根据f(sinx)+sinx﹣a=0在x∈[0,2π)上恰有两个解,利用换元法设t=sinx,t∈[﹣1,1],构造函数h(t)=2t2﹣2t+1﹣a,讨论t的取值范围,从而求出实数a的取值范围.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:
【题目】“城市呼唤绿化”,发展园林绿化事业是促进国家经济法阵和城市建设事业的重要组成部分,某城市响应城市绿化的号召,计划建一如图所示的三角形ABC形状的主题公园,其中一边利用现成的围墙BC,长度为100 ![]() 米,另外两边AB,AC使用某种新型材料围成,已知∠BAC=120°,AB=x,AC=y(x,y单位均为米).
米,另外两边AB,AC使用某种新型材料围成,已知∠BAC=120°,AB=x,AC=y(x,y单位均为米). 
(1)求x,y满足的关系式(指出x,y的取值范围);
(2)在保证围成的是三角形公园的情况下,如何设计能使所用的新型材料总长度最短?最短长度是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 的坐标分别为
的坐标分别为![]() ,直线
,直线![]() 相交于点
相交于点![]() ,且它们的斜率之积是
,且它们的斜率之积是![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() 是否存在实数
是否存在实数![]() ,使得
,使得![]() 的面积为
的面积为![]() ?若存在,请求出
?若存在,请求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(2,﹣3),
=(2,﹣3), ![]() =(﹣5,4),
=(﹣5,4), ![]() =(1﹣λ,3λ+2).
=(1﹣λ,3λ+2).
(1)若△ABC为直角三角形,且∠B为直角,求实数λ的值;
(2)若点A、B、C能构成三角形,求实数λ应满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x﹣2)2+(y﹣3)2=1交于点M、N两点.
(1)求k的取值范围;
(2)若 ![]()
![]() =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +
+ ![]() ,则下列命题中正确命题的序号是 .
,则下列命题中正确命题的序号是 .
①f(x)是偶函数;
②f(x)的值域是[ ![]() ,2];
,2];
③当x∈[0, ![]() ]时,f(x)单调递增;
]时,f(x)单调递增;
④当且仅当x=2kπ± ![]() (k∈Z)时,f(x)=
(k∈Z)时,f(x)= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,网格纸上小正方形的边长为1,粗线画出的是某个四面体的三视图,则该四面体的表面积为( ) 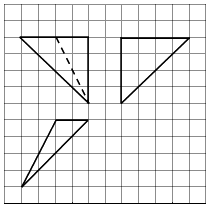
A.8+8 ![]() +4
+4 ![]()
B.8+8 ![]() +2
+2 ![]()
C.2+2 ![]() +
+ ![]()
D.![]() +
+ ![]() +
+ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() (其中
(其中![]() ,
, ![]() ),且函数
),且函数![]() 的图象在点
的图象在点![]() 处的切线与函数
处的切线与函数![]() 的图象在点
的图象在点![]() 处的切线重合.
处的切线重合.
(1)求实数![]() ,
, ![]() 的值;
的值;
(2)记函数![]() ,是否存在最小的正常数
,是否存在最小的正常数![]() ,使得当
,使得当![]() 时,对于任意正实数
时,对于任意正实数![]() ,不等式
,不等式![]() 恒成立?给出你的结论,并说明结论的合理性.
恒成立?给出你的结论,并说明结论的合理性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com