
已知扇形的圆心角为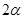 (定值),半径为
(定值),半径为 (定值),分别按图一、二作扇形的内接矩形,若按图一作出的矩形面积的最大值为
(定值),分别按图一、二作扇形的内接矩形,若按图一作出的矩形面积的最大值为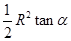 ,则按图二作出的矩形面积的最大值为
,则按图二作出的矩形面积的最大值为
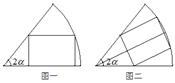
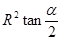
【解析】解:图一,设∠MOQ=x,则MQ=rsinx
在△OMN中,MN /sin(2α-x) =r /sin(180°-2α) ,∴MN=rsin(2α-x) /sin2α
∴矩形面积S=r2sin(2α-x) sinx/ sin2α =r2 2sin2α [cos(2x-2α)-cos2α]≤r2 2sin2α [1-cos2α]=1 /2 r2tanα
当且仅当x=α时,取得最大值,故图一矩形面积的最大值为1 2 r2tanθ,图二可拆分成两个,
图一角是2α,图二拆分后角是α,故根据图1得出的结论,可得矩形面积的最大值为
1/ 2 r2tan(θ/2)而图二时由两个这样的图形组成,所以两个则为r2tan(θ/ 2 ).
故答案为:r2tan(θ/2)


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•杭州二模)已知扇形的圆心角为2θ(0<θ<
(2012•杭州二模)已知扇形的圆心角为2θ(0<θ<| π |
| 4 |
| 1 |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com