已知95个数a1,a2,…,a95每个都只能取+1或-1两个值之一,那么它们的两两之积的和a1a2+a1a3+…+a94a95的最小正值为 .
【答案】
分析:令t=a
1a
2+a
1a
3+…+a
94a
95,进而可得2t=2(a
1a
2+a
1a
3+…+a
94a
95)=(a
1+a
2+…+a
95)
2-(a
12+a
22+…+a
952),分析易得a
12+a
22+…+a
952=95,即2t=(a
1+a
2+…+a
95)
2-95,分析a
1+a
2+…+a
95的特点,可得(a
1+a
2+…+a
95)=±11时,t取得最小值,将其代入2t=(a
1+a
2+…+a
95)
2-95中,变形可得答案.
解答:解:根据题意,令t=a
1a
2+a
1a
3+…+a
94a
95则2t=2(a
1a
2+a
1a
3+…+a
94a
95)=(a
1+a
2+…+a
95)
2-(a
12+a
22+…+a
952),
又由a
1,a
2,…,a
95每个都只能取+1或-1两个值之一,则a
12+a
22+…+a
952=95
即2t=(a
1+a
2+…+a
95)
2-95,
要使t取最小正数,t中(a
1+a
2+…+a
95)
2大于95即可,
而a
1+a
2+…+a
95为奇数个-1、1的和,不会得偶数,
则要使所求值取最小正数,须使(a
1+a
2+…+a
95)=±11,
因此t的最小值为
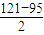
=13.
故答案为:13.
点评:本题考查等式的恒等变形的应用,解题注意转化思想,利用2(a
1a
2+a
1a
3+…+a
94a
95)=(a
1+a
2+…+a
95)
2-(a
12+a
22+…+a
952)来解题.

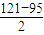 =13.
=13.

 星级口算天天练系列答案
星级口算天天练系列答案