Question

【题目】已知函数（）的图象过点，．

（1）求函数的解析式；

（2）求；

（3）解方程．

Answer 1

【答案】（1）f（x）＝4﹣2x（2）﹣5（3）

【解析】

（1）根据f（x）的图象过点A、B两点，求出b、a的值，得f（x）的解析式；

（2）由f（x）的解析式求出f（log481）的值；

（3）由f（x）的解析式化简方程f（2x）＝﹣21，求出解来即可．

解：（1）∵f（x）＝a﹣bx（b＞0）的图象过点A（2，0），B（1，2），

∴

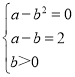
解得b＝2，a＝4；

∴函数f（x）＝4﹣2x；

（2）∵f（x）＝4﹣2x，

∴f（log481）＝4

＝4

＝4﹣9

＝﹣5；

（3）∵f（x）＝4﹣2x，

∴方程f（2x）＝﹣21可化为

4﹣22x＝﹣21，

即4+21＝22x，

∴22x＝25，

∴2x＝5，

解得x＝log25．