练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f(x)＝x2－x＋c定义在区间[0,1]上，x1，x2∈

    [0,1]，且x1≠x2，求证：

    (1)f(0)＝f(1)；

    (2)|f(x2)－f(x1)|＜|x1－x2|.

    【答案】（1）见解析； （2）见解析

    【解析】

    （1）直接计算f（0）和f（1）即可；

    （2）由于|f（x2）﹣f（x1）|=|x2﹣x1||x2+x1﹣1|．故只要证明|x2+x1﹣1|＜1即可.

    (1)∵f(0)＝c，f(1)＝c，∴f(0)＝f(1)．

    (2)|f(x2)－f(x1)|＝|x－x2＋c－x＋x1－c|＝|x2－x1||x2＋x1－1|.

    ∵0≤x1≤1,0≤x2≤1，x1≠x2，∴0＜x1＋x2＜2.

    ∴－1＜x1＋x2－1＜1.∴|x2＋x1－1|＜1.

    ∴|f(x2)－f(x1)|＜|x1－x2|.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=2sin2x+cos（2x﹣ ）．
    （Ⅰ）求f（x）的最小正周期；
    （Ⅱ）求f（x）在（0， ）上的单调递增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】椭圆C： + =1（a＞b＞0）的离心率为 ，过左焦点任作直线l，交椭圆的上半部分于点M，当l的斜率为 时，|FM|= ．
    （1）求椭圆C的方程；
    （2）椭圆C上两点A，B关于直线l对称，求△AOB面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，过其右焦点F且与x轴垂直的直线交椭圆C于P，Q两点，椭圆C的右顶点为R，且满足.

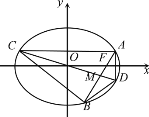
    (1)求椭圆C的方程；

    (2)若斜率为k(其中)的直线l过点F，且与椭圆交于点A，B，弦AB的中点为M，直线OM与椭圆交于点C，D，求四边形ACBD面积的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线和的焦点分别为， 交于O,A两点（O为坐标原点），且

    （Ⅰ）求抛物线的方程；

    （Ⅱ）过点O的直线交的下半部分于点M，交的左半部分于点N，点，求面积的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某渔业公司今年初用98万元购进一艘渔船用于捕捞，第一年需各种费用12万

    元，从第二年开始包括维修费在内，每年所需费用均比上一年增加4万元，该船每年捕捞的

    总收入为50万元.

    （1）该船捕捞几年开始盈利(即总收入减去成本及所有费用之差为正值)？

    （2）该船捕捞若干年后，处理方案有两种：

    ①当年平均盈利达到最大值时，以26万元的价格卖出;

    ②当盈利总额达到最大值时，以8万元的价格卖出.问哪一种方案较为合算，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=2 sin（ax﹣ ）cos（ax﹣ ）+2cos2（ax﹣ ）（a＞0），且函数的最小正周期为 ．
    （Ⅰ）求a的值；
    （Ⅱ）求f（x）在[0， ]上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】闽越水镇是闽侯县打造闽都水乡文化特色小镇核心区，该小镇有一块1800平方米的矩形地块，开发商准备在中间挖出三个矩形池塘养闽侯特色金鱼，挖出的泥土堆在池塘四周形成基围(阴影部分所示)种植柳树，形成柳中观鱼特色景观．假设池塘周围的基围宽均为2米，如图，设池塘所占的总面积为平方米．

    (1)试用表示a及；

    (2)当取何值时，才能使得最大？并求出的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[选修4-5：不等式选讲]
    设函数f（x）=|2x+2|﹣|x﹣2|．
    （Ⅰ）求不等式f（x）＞2的解集；
    （Ⅱ）若x∈R，f（x）≥t2﹣ t恒成立，求实数t的取值范围．

    查看答案和解析>>

    同步练习册答案