
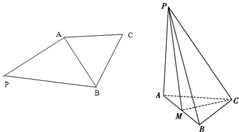
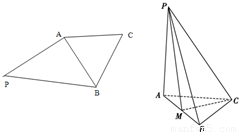
 如图所示,平面四边形PABC中,∠PAB为直角,△ABC为等边三角形,现把△PAB沿着AB折起,使得△APB与△ABC垂直,且点M为AB的中点.
如图所示,平面四边形PABC中,∠PAB为直角,△ABC为等边三角形,现把△PAB沿着AB折起,使得△APB与△ABC垂直,且点M为AB的中点.| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| hB |
| BC |
| ||||
| 2a |
| ||
| 4 |
| 1-sin2θ |
1-(
|
| ||
| 4 |


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
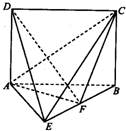
 如图所示,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC
如图所示,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC
| 1 |
| 2 |

| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知几何体E-ABCD如图所示,其中四边形ABCD为矩形,△ABE为等边三角形,且AD=
已知几何体E-ABCD如图所示,其中四边形ABCD为矩形,△ABE为等边三角形,且AD=| 3 |
| 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
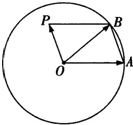 已知单位圆O上的两点A,B及单位圆所在平面上的一点P,满足
已知单位圆O上的两点A,B及单位圆所在平面上的一点P,满足| OP |
| OA |
| OB |
| OP |
| OA |
| OB |
| 1 |
| 3 |
| OD |
| OA |
查看答案和解析>>
科目:高中数学 来源:2013年浙江省杭州市重点高中高考命题比赛数学参赛试卷13(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com