
【题目】选修4-5:不等式选讲
已知函数![]()
(1)求不等式![]() 的解集
的解集![]() ;
;
(2)若![]() ,求证:
,求证: ![]() .
.
 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】如图,在空间几何体A﹣BCDE中,底面BCDE是梯形,且CD∥BE,CD=2BE=4,∠CDE=60°,△ADE是边长为2的等边三角形,F为AC的中点. (Ⅰ)求证:BF∥平面ADE;
(Ⅱ)若AC=4,求证:平面ADE⊥平面BCDE;
(Ⅲ)若AC=4,求几何体C﹣BDF的体积.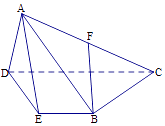
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年春节期间,某服装超市举办了一次有奖促销活动,消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.
方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸出2个红球则打6折,若摸出1个红球,则打7折;若没摸出红球,则不打折.
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)五边形![]() 中,
中, ![]()
![]() ,将
,将![]() 沿
沿![]() 折到
折到![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() ,如图(2),点
,如图(2),点![]() 为线段
为线段![]() 的中点,且
的中点,且![]() 平面
平面![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与所成角的正切值为
与所成角的正切值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:参数方程与极坐标系
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() 为倾斜角),以坐标原点O为极点,
为倾斜角),以坐标原点O为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线![]() 的直角坐标方程,并 求C的焦点F的直角坐标;
的直角坐标方程,并 求C的焦点F的直角坐标;
(2)已知点![]() ,若直线
,若直线![]() 与C相交于A,B两点,且
与C相交于A,B两点,且![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的偶函数,在[0,+∞)上单调递增.若a=f(log ![]()
![]() ),b=f(log
),b=f(log ![]()
![]() ),c=f(﹣2),则a,b,c的大小关系是( )
),c=f(﹣2),则a,b,c的大小关系是( )
A.a>b>c
B.b>c>a
C.c>b>a
D.c>a>b
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】种子发芽率与昼夜温差有关.某研究性学习小组对此进行研究,他们分别记录了3月12日至3月16日的昼夜温差与每天100颗某种种子浸泡后的发芽数,如下表:

(I)从3月12日至3月16日中任选2天,记发芽的种子数分别为c,d,求事件“c,d均不小于25”的概率;
(II)请根据3月13日至3月15日的三组数据,求出y关于x的线性回归方程![]() ;
;
(III)若由线性回归方程得到的估计数据与实际数据误差均不超过2颗,则认为回归方程是可靠的,试用3月12日与16日的两组数据检验,(II)中的回归方程是否可靠?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com