
����Ŀ����Դ�����³ǽ�һ���ţ����˵��Ŷ��ѽ��ã����������![]() �ף����¹���ֻ�轨�����Ŷ�֮���������Ŷգ���Ԥ�⣬һ���ŶյĹ��̷���Ϊ32��Ԫ������Ϊx����������֮������湤�̷���Ϊ
�ף����¹���ֻ�轨�����Ŷ�֮���������Ŷգ���Ԥ�⣬һ���ŶյĹ��̷���Ϊ32��Ԫ������Ϊx����������֮������湤�̷���Ϊ![]() ��Ԫ�������ŶյȾ���ֲ��������Ŷն���Ϊ�㣬�Ҳ������������أ������¹��̵ķ���Ϊ
��Ԫ�������ŶյȾ���ֲ��������Ŷն���Ϊ�㣬�Ҳ������������أ������¹��̵ķ���Ϊ![]() ��Ԫ��
��Ԫ��
��1�����![]() ����
����![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2����![]() ��96�������½����ٸ��Ŷղ���ʹ���¹��̵ķ���
��96�������½����ٸ��Ŷղ���ʹ���¹��̵ķ���![]() ��С��
����
���𰸡���1��![]() ����2�����½�
����2�����½�![]() ���Ŷղ���ʹ���¹��̵ķ���
���Ŷղ���ʹ���¹��̵ķ���![]() ��С.
��С.
��������
�����������1��������������Ŷպ����湤������Ȼ��������⽨�������ܷ����빤�����ĺ�����ϵ����2����![]() ����ʱ��������֪��������ʽ�������ʱ�ĺ�������ʽ���������ݵ����뺯�������ԵĹ�ϵ�����ֵ�Լ���ʱ
����ʱ��������֪��������ʽ�������ʱ�ĺ�������ʽ���������ݵ����뺯�������ԵĹ�ϵ�����ֵ�Լ���ʱ![]() ��ֵ.
��ֵ.
���������(1)�����½�n���Ŷգ���(n+1)x=m����![]()
����![]()
=![]()
(2)��![]() ʱ��
ʱ��![]()
��![]()
��![]() ����
����![]() ������x=16
������x=16
��0<x<16ʱ��![]() ��
��![]() ������(0,16)����������
������(0,16)����������
��16<x<96��![]() ��
��![]() ������(16,96)����������
������(16,96)����������
����![]() ��
��![]() =16��ȡ����Сֵ����ʱ
=16��ȡ����Сֵ����ʱ![]()
�����½�5���Ŷղ���ʹ���¹��̵ķ���![]() ��С.
��С.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=![]() �Ķ�����Ϊ��-1��1��������f��-x��=-f��x������
�Ķ�����Ϊ��-1��1��������f��-x��=-f��x������![]() ��
��
��1������f��x���Ľ���ʽ��
��2��֤��f��x���ڣ�-1��1��������������
��3���ⲻ��ʽ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��![]() ������ʽѡ��
������ʽѡ��
��֪����f��x��=|2x+3|+|2x��1|��
������ʽf��x����8�Ľ⼯��
����������x�IJ���ʽf��x����|3m+1|�н⣬��ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017��ӱ�ʡ������ѧ������ѧ�ڵ������¿������У���ѧ����������ƽ��ֱ������ϵ�У���![]() ����ԭ��ʱ������
����ԭ��ʱ������![]() �ġ�����㡱Ϊ
�ġ�����㡱Ϊ![]() ����
����![]() ��ԭ��ʱ������
��ԭ��ʱ������![]() �ġ�����㡱Ϊ��������ƽ������
�ġ�����㡱Ϊ��������ƽ������![]() �����е�ġ�����㡱�����ɵ�����
�����е�ġ�����㡱�����ɵ�����![]() ����Ϊ����
����Ϊ����![]() �ġ��������ߡ��������������⣺
�ġ��������ߡ��������������⣺
������![]() �ġ�����㡱�ǵ�
�ġ�����㡱�ǵ�![]() �����
�����![]() �ġ�����㡱�ǵ�
�ġ�����㡱�ǵ�![]() ��
��
��������![]() ����
����![]() ��Գƣ����䡰�������ߡ�
��Գƣ����䡰�������ߡ� ![]() ����
����![]() ��Գƣ�
��Գƣ�
�۵�λԲ�ġ��������ߡ�����������
��һ��ֱ�ߵġ��������ߡ���һ��ֱ��.
����������ĸ���Ϊ�� ��
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �ϵĺ���
�ϵĺ���![]() ��ͼ����
��ͼ����![]() ����
����![]() ������
������![]() �����ݼ�����֪����
�����ݼ�����֪����![]() Ϊż�����������
Ϊż�����������![]() �IJ���ʽ
�IJ���ʽ![]() �Ľ�Ϊ �� ��
�Ľ�Ϊ �� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ����A��B���ֲ�Ʒ�������г��������г�Ԥ�⣬֪A��Ʒ��������Ͷ�ʳ����ȣ����ϵ��ͼ1��B��Ʒ��������Ͷ�ʵ�����ƽ���������ȣ����ϵ��ͼ2.(ע����ʾͼ�еĺ������ʾͶ�ʽ���λ����Ԫ)

ͼ1 ͼ2
��1���ֱ�A��B���ֲ�Ʒ�������ʾΪͶ�ʵĺ�����ϵʽ��
��2������ҵ�ѳO10��Ԫ�ʽ𣬲�ȫ��Ͷ��A��B���ֲ�Ʒ���������ʣ�����������10��Ԫ�ʽ𣬲���ʹ��ҵ�����������������Ϊ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijҽҩ�о���������һ��ҩ����������˰��涨�ļ������ã��ݼ�⣬��ҩ��ÿ�����еĺ�ҩ��![]() ���ˣ���ʱ��
���ˣ���ʱ��![]() ��Сʱ��֮�����������ͼ��ʾ������.����
��Сʱ��֮�����������ͼ��ʾ������.����![]() ʱ��
ʱ�� ![]() ��.
��.
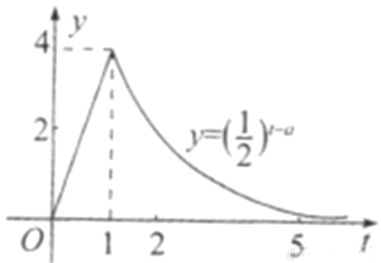
��1��д����һ�η�ҩ��![]() ��
��![]() ֮��ĺ�����ϵʽ
֮��ĺ�����ϵʽ![]() ��
��
��2���ݽ�һ���ⶨ��ÿ����ѪҺ�к�ҩ��������![]() ��ʱ�����Ƽ�����Ч�����ҩһ�κ����Ƽ�����Чʱ��.
��ʱ�����Ƽ�����Ч�����ҩһ�κ����Ƽ�����Чʱ��.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com