
| A. | 6 | B. | 7 | C. | 9 | D. | 10 |
分析 求出函数f(x)的导数,求出f(x)的单调区间,从而求出其零点的范围,求出f(x-1)的零点所在的范围;通过讨论x的范围,求出g(x)在(0,+∞)的导数,得到g(x)的单调区间,结合函数的奇偶性求出所有零点所在的区间,从而求出g(x+1)所在的零点的范围,进而求出a,b的值,求出答案即可.
解答 解:∵f′(x)=1-x+x2-x3+…-x2015=$\frac{1{-x}^{2016}}{1+x}$,
令f′(x)>0,解得:x<1且x≠-1,令f′(x)<0,解得:x>1,
∴f(x)在(-∞,-1)递递增,在(-1,1)递增,在(1,+∞)递减,
而f(0)=1>0,f(-1)=1-1-$\frac{1}{2}$-$\frac{1}{3}$-…-$\frac{1}{2016}$<0,
∴函数f(x)在区间(-1,0)内有零点,
f(1)=1+(1-$\frac{1}{2}$)+($\frac{1}{3}$-$\frac{1}{4}$)+…+($\frac{1}{2015}$-$\frac{1}{2016}$)>0,
f(2)=1-23($\frac{1}{2}$-$\frac{1}{3}$)-25($\frac{1}{3}$-$\frac{1}{5}$)-27($\frac{1}{4}$-$\frac{1}{7}$)-…-22015($\frac{1}{1008}$-$\frac{1}{2015}$)<0,
∴函数f(x)在区间(1,2)内有零点,
故函数f(x)在(-1,2)有2个零点,
∴-1<x-1<2,∴0<x<3;
g(x)=ln|x|+|x|-2,
当x>0时,g(x)=lnx+x-2,g′(x)=$\frac{1}{x}$+1>0,
∴g(x)在(0,+∞)递增,
而g(1)=-1<0,g(2)=ln2>0,
∴x>0时,g(x)在(1,2)存在唯一零点,
∵g(x)是偶函数,
∴g(x)在(-∞,0)递减,
而g(-1)=-1<0,g(-2)=ln2>0,
∴x<0时,g(x)在(-2,-1)存在唯一零点,
∴g(x)在(-2,2)存在零点.
∴-2<x<2,∴-2<x+1<2,即-3<x<1,
综上-3<x<3,
∴a=-3,b=3,b-a=6,
故选:A.
点评 本题考查了函数的单调性、极值问题,考查函数的奇偶性问题,考查导数的应用以及数列求和问题,是一道综合题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
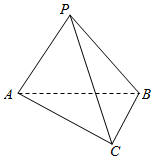 如图,把等腰直角三角形ABC以斜边AB为轴旋转,使C点移动的距离等于AC时停止,并记为点P.
如图,把等腰直角三角形ABC以斜边AB为轴旋转,使C点移动的距离等于AC时停止,并记为点P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
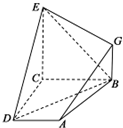 如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且$∠BCD=∠BCE=\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2
如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且$∠BCD=∠BCE=\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
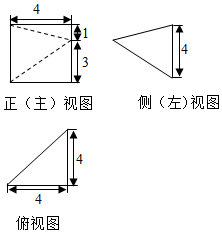 一锥体的三视图如图所示,设该棱锥的最长棱和最短棱的棱长分别为m,n,则$\frac{m}{n}$等于( )
一锥体的三视图如图所示,设该棱锥的最长棱和最短棱的棱长分别为m,n,则$\frac{m}{n}$等于( )| A. | $\frac{\sqrt{33}}{4}$ | B. | $\frac{\sqrt{41}}{3}$ | C. | $\frac{\sqrt{41}}{4}$ | D. | $\frac{\sqrt{33}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com