
设 ,
,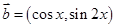 ,
,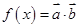 .(1)求
.(1)求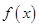 的最小正周期、最大值及
的最小正周期、最大值及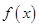 取最大值时
取最大值时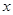 的集合;
的集合;
(2)若锐角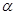 满足
满足 ,求
,求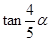 的值.
的值.
(1)函数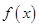 的最小正周期为
的最小正周期为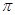 ,最大值为
,最大值为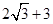 ,
,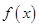 取最大值时
取最大值时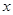 的集合为
的集合为 ;(2)
;(2) .
.
解析试题分析:(1)先利用平面向量数量积结合二倍角降幂公式以及辅助角公式将函数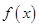 的解析式化为
的解析式化为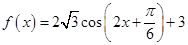 ,然后利用相关公式求出函数
,然后利用相关公式求出函数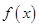 的最小正周期,并令
的最小正周期,并令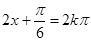
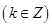 求出函数
求出函数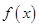 的最大值以及取最大值时
的最大值以及取最大值时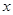 的取值集合;(2)先利用已知条件
的取值集合;(2)先利用已知条件 并结合角
并结合角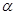 为锐角这一条件求出角
为锐角这一条件求出角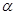 的值,并最终求出
的值,并最终求出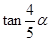 的值.
的值.
试题解析:(1)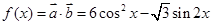 1分
1分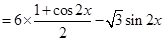
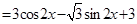
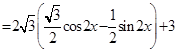 3分
3分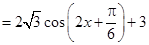 4分 最小正周期
4分 最小正周期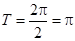 5分
5分
当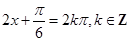 ,即
,即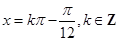 时,
时,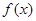 有最大值
有最大值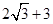 ,
,
此时,所求x的集合为 . 7分
. 7分
(2)由 得
得 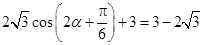 ,故
,故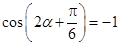 9分
9分
又由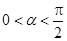 得
得 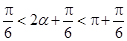 , 故
, 故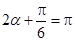 ,解得
,解得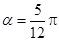 . 11分
. 11分
从而 . 12分
. 12分
考点:1.平面向量的数量积的坐标表示;2.二倍角的降幂公式;3.辅助角公式;4.三角函数的周期性与最值


 字词句段篇系列答案
字词句段篇系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com