练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知圆满足①截y轴所得弦长为2，②被x轴分成两段圆弧，其弧长的比为3∶1，③圆心到直线l：x－2y=0的距离为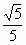．求该圆的方程．

    答案：
    解析：

    解:设所求圆P的圆心P(a，b)，半径为r，由题设知圆P截x轴所得劣弧的圆心角为．又圆P截y轴所得弦长为2，∴＋1，∴即a－2b=±1，上述两个方程联立可得．所求圆的方程是=2．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知动圆P：（x-a）2+（y-b）2=r2（r＞0）被y轴所截的弦长为2，被x轴分成两段弧，且弧长之比等于
    13
     ， |OP|≤r    （其中P（a，b）为圆心，O为坐标原点）．
    （1）求a，b所满足的关系式；
    （2）点P在直线x-2y=0上的投影为A，求事件“在圆P内随机地投入一点，使这一点恰好在△POA内”的概率的最大值．

    查看答案和解析>>

    科目：高中数学 来源：天津市新人教A版数学2012届高三单元测试32：直线和圆 题型：044

    已知动圆P：(x－a)2＋(y－b)2＝r2(r＞0)被y轴所截的弦长为2，被x轴分成两段弧，且弧长之比等于，|OP|≤r(其中点P(a，b)为圆心，o为坐标原点)

    (1)求a，b所满足的关系；

    (2)点P在直线x－2y＝0上的投影为A，求事件“在圆P内随机地投入一点，使这一点恰好落在△POA内”的概率的最大值．

    查看答案和解析>>

    科目：高中数学 来源：导学大课堂必修二数学苏教版 苏教版 题型：044

    已知圆C在y轴上截得的弦长为2，在x轴上截得的弦长为4．

    (1)求圆心C的坐标所满足的关系式；

    (2)求当圆心C到点M(0，2)的距离d最小时的圆的方程．

    查看答案和解析>>

    科目：高中数学 来源：2014届湖北武汉部分重点中学高二上学期期末考试文科数学卷（解析版） 题型：解答题

    （本小题15分）已知动圆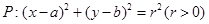被y轴所截的弦长为2，被x轴分成两段弧，且弧长之比等于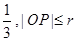（其中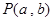为圆心，O为坐标原点）。

    （1）求a，b所满足的关系式；

    （2）点P在直线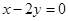上的投影为A，求事件“在圆P内随机地投入一点，使这一点恰好在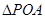内”的概率的最大值

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年湖北省武汉市部分重点中学高二（上）期末数学试卷（文科）（解析版） 题型：解答题

    已知动圆P：（x-a）2+（y-b）2=r2（r＞0）被y轴所截的弦长为2，被x轴分成两段弧，且弧长之比等于（其中P（a，b）为圆心，O为坐标原点）．
    （1）求a，b所满足的关系式；
    （2）点P在直线x-2y=0上的投影为A，求事件“在圆P内随机地投入一点，使这一点恰好在△POA内”的概率的最大值．

    查看答案和解析>>

    同步练习册答案