
【题目】已知△ABC的三个内角A,B,C所对的边分别为a,b,c,若三个内角A,B,C成等差数列,且a= ![]() ,b=
,b= ![]() ,求sinC的值.
,求sinC的值.
【答案】解:∵三个内角A,B,C成等差数列,
∴2B=A+C,
∵A+B+C=π,
∴3B=π,即B= ![]() ,
,
∵a= ![]() ,b=
,b= ![]() ,
,
∴由正弦定理 ![]() 得:sinA=
得:sinA= ![]() =
= 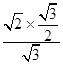 =
= ![]() ,
,
∵a<b,∴A<B,即A= ![]() ,
,
则sinC=sin(A+B)=sinAcosB+cosAsinB= ![]() ×
× ![]() +
+ ![]() ×
× ![]() =
= ![]()
【解析】由三内角成等差数列及内角和定理求出B的度数,再由a与b的值,利用正弦定理求出sinA的值,确定出A的度数,由sinC=sin(A+B),利用两角和与差的正弦函数公式化简,将A与B的度数代入计算即可求出值.
【考点精析】通过灵活运用正弦定理的定义和余弦定理的定义,掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= ![]() (0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值及f(x)的表达式.
(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩,被抽取学生的成绩均不低于160分,且低于185分,如图是按成绩分组得到的频率分布直方图. 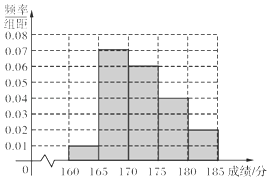
(1)为了能选拔出优秀的学生,该校决定在笔试成绩较高的第3组、第4组、第5组中用分层抽样的方法抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试;
(2)在(1)的前提下,学校决定在6名学生中随机抽取2名学生由考官A面试,求第4组至少有一名学生被考官A面试的概.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道Ⅲ绕月飞行,若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:
①a1+c1=a2+c2;②a1﹣c1=a2﹣c2;③c1a2>a1c2;④ ![]() .
.
其中正确式子的序号是( )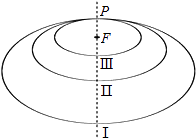
A.①③
B.②③
C.①④
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() 的两个焦点为
的两个焦点为 ![]()
的曲线C上.
(1)求双曲线C的方程;
(2)记O为坐标原点,过点Q(0,2)的直线l与双曲线C相交于不同的两点E、F,若△OEF的面积为2 ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a<1,集合A={x∈R|x>0},B={x∈R|2x2﹣3(1+a)x+6a>0},D=A∩B.
(1)求集合D(用区间表示);
(2)求函数f(x)=x2﹣(1+a)x+a在D内的零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出1个该产品获利润5元,未售出的产品,每个亏损3元.根据历史资料,得到开学季市场需求量的频率分布直方图如图所示.该同学为这个开学季购进了160个该产品,以![]() (
(![]() ,单位:个)表示这个开学季内的市场需求量.
,单位:个)表示这个开学季内的市场需求量.
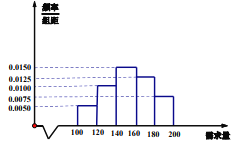
(1)根据直方图估计这个开学季内市场需求量![]() 的中位数;
的中位数;
(2)根据直方图估计利润不少于640元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com