
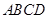 中,
中,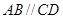 ,
,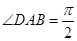 ,点
,点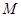 、
、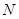 分别在
分别在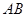 ,
,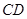 上,且
上,且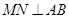 ,
,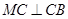 ,
, ,
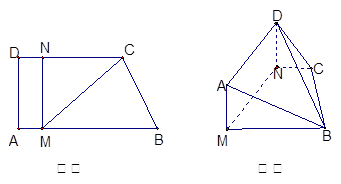
,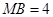 ,现将梯形
,现将梯形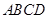 沿
沿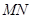 折起,使平面
折起,使平面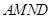 与平面
与平面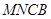 垂直(如图乙).
垂直(如图乙).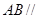 平面
平面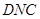 ;
;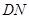 的长为何值时,二面角
的长为何值时,二面角 的大小为
的大小为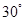 ?
?
 平面DNC,NC
平面DNC,NC 平面DNC,
平面DNC, MB//平面DN C.…………………2分
MB//平面DN C.…………………2分 MB="M," 且MA,MB
MB="M," 且MA,MB 平面MA B.
平面MA B.
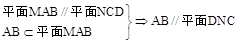 . (6分)
. (6分) 交BC延长线于H,连HN,
交BC延长线于H,连HN, 平面AMND
平面AMND 平面MNCB,DN
平面MNCB,DN MN, …………………8分
MN, …………………8分 DN
DN 平面MBCN,从而
平面MBCN,从而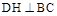 ,
,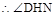 为二面角D-BC-N的平面角.
为二面角D-BC-N的平面角. 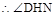 =
=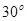 …………………10分
…………………10分  知
知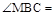 60º,
60º, .
.  sin60º =
sin60º = …………………11分
…………………11分 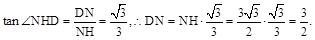 …………………12分
…………………12分  轴,
轴,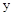 轴和
轴和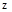 轴,建立空间直角坐标系
轴,建立空间直角坐标系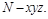 易得NC=3,MN=
易得NC=3,MN=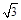 ,
, ,则
,则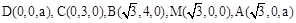 .
.
 .
.
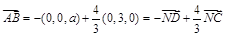 ,
,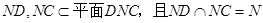 ,
, 与平面
与平面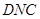 共面,又
共面,又 ,
,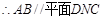 . (6分)
. (6分)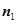
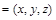 ,
,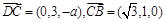
 ,令
,令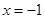 ,则
,则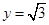 ,
,
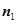
 . (8分)
. (8分)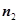
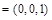 . (9分)
. (9分)

 …………………11分
…………………11分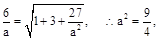 又
又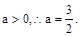 即
即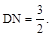 …………………12分
…………………12分

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源:不详 题型:单选题
 、
、 、
、 表示三条不同的直线,
表示三条不同的直线, 表示平面,给出下列命题:
表示平面,给出下列命题: ∥
∥ ,
, ∥
∥ ,则
,则 ∥
∥ ;②若
;②若 ⊥
⊥ ,
, ⊥
⊥ ,则
,则 ⊥
⊥ ;
; ∥
∥ ,
, ∥
∥ ,则
,则 ∥
∥ ;④若
;④若 ⊥
⊥ ,
, ⊥
⊥ ,则
,则 ∥
∥ ;则其中正确的是( )
;则其中正确的是( )| A.①② | B.②③ | C.①④ | D.③④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
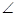 BAD=
BAD=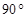 ,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点.
,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点.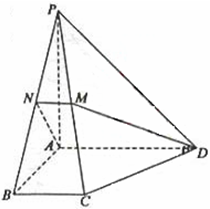
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
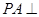 矩形ABCD所在平面,PA=AD=
矩形ABCD所在平面,PA=AD=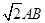 ,E为线段PD上一点,G为线段PC的中点.
,E为线段PD上一点,G为线段PC的中点.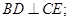
 时,求证:BG//平面AEC.
时,求证:BG//平面AEC.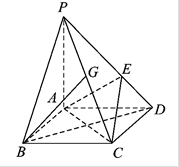
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
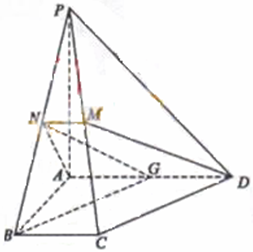
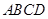 中,
中,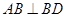 ,
,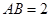 ,
,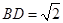 ,沿
,沿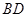 将
将 折
折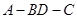 是大小为锐角
是大小为锐角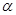 的二面角,设
的二面角,设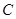 在平面
在平面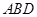 上的射影为
上的射影为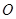 .
.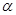 为何值时,三棱锥
为何值时,三棱锥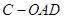 的体积最大?最大值为多少?
的体积最大?最大值为多少?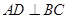 时,求
时,求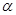 的大小.
的大小.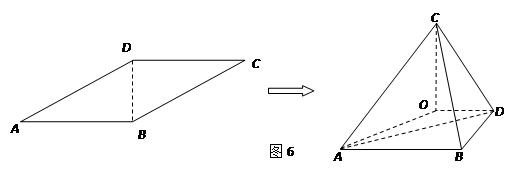
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
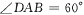 .
.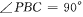 ;
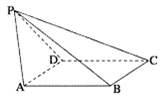
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com