

(2)若P是棱长均为a的正四面体S—ABC内任意一点,试证明点P到各侧面的距离之和为定值.
思路解析:(1)连结PA、PB、PC,将正三角形分割成三个小三角形,利用三角形面积不变即可求得点P到各边的距离之和为定值.
(2)运用“类比”法进行求解.平面→空间:正三角形→正四面体;面积→体积;分割→分割;内分小三角形→内分小四面体;小三角形一边长→四面体底面积.于是可将正四面体S—ABC分割成四个以点P为顶点,四个面为底面的小三棱锥.利用正四面体的体积不变求得点P到各侧面的距离之和为定值.
(1)证明:设P到各边的距离分别为m、l、n,则有△ABC的面积等于三个小三角形△APC、△APB、△BPC的面积的和,列式即为
S△ABC=S△APC+S△APB+S△BPC=![]() al+
al+![]() am+
am+![]() an=
an=![]() a(l+m+n)=
a(l+m+n)=![]() a2,
a2,
得到l+m+n=![]() a.
a.

(2)解:设P到四面体各面的距离分别为m、l、n、h,则四面体SABC的体积等于四个小四面体P—ABC、P—SBC、P—SAC、P—SAB的体积之和,列式计算即为
VS—ABC=VP—ABC+VP—SBC+VP—SAC+VP—SAB=![]() ·
·![]() a2·(l+m+n+h)=
a2·(l+m+n+h)=![]() a3.
a3.
得到l+m+n+h=a.
方法归纳 用等积法求点到平面的距离的步骤:
(1)设距离为h,把h看成某三棱锥的高;
(2)把三棱锥的另一面看成底面,求出体积;
(3)由体积相等求出相应的距离.


科目:高中数学 来源: 题型:
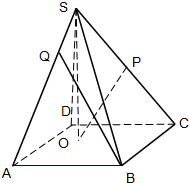 如图,已知四棱锥S-ABCD的底面是边长为4的正方形,S在底面上的射影O落在正方形ABCD内,SO的长为3,O到AB,AD的距离分别为2和1,P是SC的中点.
如图,已知四棱锥S-ABCD的底面是边长为4的正方形,S在底面上的射影O落在正方形ABCD内,SO的长为3,O到AB,AD的距离分别为2和1,P是SC的中点.| AQ |
| 3 |
| 4 |
| AS |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•日照一模)如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中
(2013•日照一模)如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中| AP |
| AB |
| AE |
查看答案和解析>>
科目:高中数学 来源:2007年普通高等学校招生全国统一考试、文科数学(上海卷) 题型:044
我们把由半椭圆![]() (x≥0)与半椭圆
(x≥0)与半椭圆![]() (x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0.
(x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0.
如图,设点F0,F1,F2是相应椭圆的焦点,A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点.

(1)若△F0F1F2是边长为1的等边三角形,求该“果圆”的方程;
(2)设P是“果圆”的半椭圆![]() (x≤0)上任意一点.求证:当|PM|取得最小值时,P在点B1,B2或A1处;
(x≤0)上任意一点.求证:当|PM|取得最小值时,P在点B1,B2或A1处;
(3)若P是“果圆”上任意一点,求|PM|取得最小值时点P的横坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com