
【题目】已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=x2﹣2x. 
(1)画出偶函数f(x)的图像的草图,并求函数f(x)的单调递增区间;
(2)当直线y=k(k∈R)与函数y=f(x)恰有4个交点时,求k的取值范围.
【答案】
(1)解:画出f(x)的图像如下图:

由图像知,函数f(x)单调递增区间为[﹣1,0],[1,+∞)
(2)解:由图像可知,当﹣1<k<0时,直线与函数y=f(x)的图像的交点个数为4;
∴k的取值范围为(﹣1,0)
【解析】(1)根据已知条件画出函数f(x)的图像,根据图像即可得到f(x)的单调递增区间;(2)通过图像即可得到k的取值范围.
【考点精析】解答此题的关键在于理解函数奇偶性的性质的相关知识,掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇,以及对二次函数的性质的理解,了解当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:
【题目】海岛B上有一座高为10米的塔,塔顶的一个观测站A,上午11时测得一游船位于岛北偏东15°方向上,且俯角为30°的C处,一分钟后测得该游船位于岛北偏西75°方向上,且俯角45°的D处(假设游船匀速行驶).
(1)求该船行驶的速度(单位:米/分钟).
(2)又经过一段时间后,游船到达海岛B的正西方向E处,问此时游船距离海岛B多远.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司在迎新年晚会上举行抽奖活动,有甲、乙两个抽奖方案供员工选择;
方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率为![]() .第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
.第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
方案乙:员工连续三次抽奖,每次中奖率均为![]() ,每次中奖均可获奖金400元.
,每次中奖均可获奖金400元.
(1)求某员工选择方案甲进行抽奖所获奖金![]() (元)的分布列;
(元)的分布列;
(2)某员工选择方案乙与选择方案甲进行抽奖,试比较哪个方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集合M={x|﹣2≤x≤2},N={y|0≤y≤2},给出下列四个图形,其中能表示以M为定义域,N为值域的函数关系的是( )
A.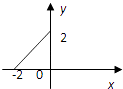
B.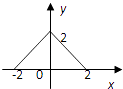
C.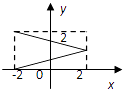
D.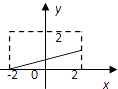
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=max{x2﹣ax+a,ax﹣a+1},其中max{x,y}= ![]() . (Ⅰ)若对任意x∈R,恒有f(x)=x2﹣ax+a,求实数a的值;
. (Ⅰ)若对任意x∈R,恒有f(x)=x2﹣ax+a,求实数a的值;
(Ⅱ)若a>1,求f(x)的最小值m(a).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com