
【题目】已知函数f(x)=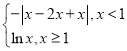 ,若对于t∈R,f(t)≤kt恒成立,则实数k的取值范围是________.
,若对于t∈R,f(t)≤kt恒成立,则实数k的取值范围是________.
【答案】[![]() ,1]
,1]
【解析】
本题条件“t∈R,f(t)≤kt”的几何意义是:在(-∞,+∞)上,函数y=f(t)的图像恒在直线y=kt的下方,利用数形结合的方法解决本问题.
令y=x3-2x2+x,x<1,则y′=3x2-4x+1=(x-1)·(3x-1),
令y′>0,即(x-1)(3x-1)>0,解得x<![]() 或x>1.又因为x<1,所以x<
或x>1.又因为x<1,所以x<![]() .
.
令y′<0,得![]() <x<1.
<x<1.
所以y的增区间是(-∞![]() ),减区间是(
),减区间是(![]() ,1),所以y极大值=
,1),所以y极大值=![]() .
.
根据图像变换可作出函数y=-|x3-2x2+x|,x<1的图像.
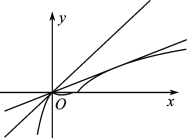
又设函数y=lnx(x≥1)的图像经过原点的切线斜率为k1,切点(x1,lnx1),
因为y′=![]() ,所以k1=
,所以k1=![]() =
=![]() ,解得x1=e,所以k1=
,解得x1=e,所以k1=![]() .
.
函数y=x3-2x2+x在原点处的切线斜率k2=y′x=0=1.
因为t∈R,f(t)≤kt,所以根据f(x)的图像,数形结合可得![]() ≤k≤1.
≤k≤1.


科目:高中数学 来源: 题型:
【题目】(本小题满分12分)如图,三棱柱ABC-A1B1C1中,CA=CB,AB=A A1,∠BA A1=60°.
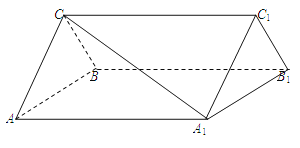
(Ⅰ)证明AB⊥A1C;
(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C 与平面BB1C1C所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一所高中为备战即将举行的全市羽毛球比赛,学校决定组织甲、乙两队进行羽毛球对抗赛实战训练.每队四名运动员,并统计了以往多次比赛成绩,按由高到低进行排序分别为第一名、第二名、第三名、第四名.比赛规则为甲、乙两队同名次的运动员进行对抗,每场对抗赛都互不影响,当甲、乙两队的四名队员都进行一次对抗赛后称为一个轮次.按以往多次比赛统计的结果,甲、乙两队同名次进行对抗时,甲队队员获胜的概率分别为![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)进行一个轮次对抗赛后一共有多少种对抗结果?
(2)计分规则为每次对抗赛获胜一方所在的队得1分,失败一方所在的队得0分,设进行一个轮次对抗赛后甲队所得分数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() ,
,![]() ,
,![]() .
.
(1)设![]() ,假设
,假设![]() 在
在![]() 上递减,求
上递减,求![]() 的取值范围;
的取值范围;
(2)假设![]() ,求证:
,求证:![]() .
.
(3)是否存在实数![]() ,使得
,使得![]() 恒成立,假设存在,求出
恒成立,假设存在,求出![]() 的取值范围,假设不存在,请说明理由.
的取值范围,假设不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,
的等差数列,![]() 是首项为
是首项为![]() ,公比为q的等比数列.
,公比为q的等比数列.
(1)设![]() ,若
,若![]() 对
对![]() 均成立,求d的取值范围;
均成立,求d的取值范围;
(2)若![]() ,证明:存在
,证明:存在![]() ,使得
,使得![]() 对n=2,3,···,m+1均成立,并求d的取值范围(用
对n=2,3,···,m+1均成立,并求d的取值范围(用![]() 表示).
表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)求函数![]() 的单调增区间;
的单调增区间;
(2)令![]() ,且函数
,且函数![]() 有三个彼此不相等的零点
有三个彼此不相等的零点![]() ,其中
,其中![]() .
.
①若![]() ,求函数
,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
②若对![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴的建立极坐标系,曲线
轴正半轴为极轴的建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)若点![]() 与点
与点![]() 分别为曲线
分别为曲线![]() 动点,求
动点,求![]() 的最小值,并求此时的
的最小值,并求此时的![]() 点坐标.
点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为该椭圆的一条垂直于
为该椭圆的一条垂直于![]() 轴的动弦,直线
轴的动弦,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() .
.
(1)证明:点![]() 恒在椭圆
恒在椭圆![]() 上.
上.
(2)设直线![]() 与椭圆
与椭圆![]() 只有一个公共点
只有一个公共点![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,在平面内是否存在定点
,在平面内是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出该点坐标;若不存在,说明理由.
恒成立?若存在,求出该点坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com