
 如图,在正方体ABCD-A1B1C1D1中,点O为线段BD的中点.设点P在线段B1C1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( )
如图,在正方体ABCD-A1B1C1D1中,点O为线段BD的中点.设点P在线段B1C1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( )| A. | $[\frac{{\sqrt{6}}}{3},1]$ | B. | $[\frac{{\sqrt{2}}}{3},1]$ | C. | $[\frac{{\sqrt{2}}}{3},\frac{{2\sqrt{2}}}{3}]$ | D. | $[\frac{{\sqrt{6}}}{3},\frac{{2\sqrt{2}}}{3}]$ |
分析 设正方体的棱长为2,以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出sinα的取值范围.
解答 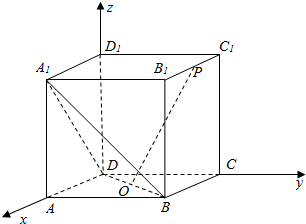 解:设正方体的棱长为2,
解:设正方体的棱长为2,
以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
则A1(2,0,2),B(2,2,0),D(0,0,0),O(1,1,0),ymc P(a,2,2),0≤a≤2,
$\overrightarrow{D{A}_{1}}$=(2,0,2),$\overrightarrow{DB}$=(2,2,0),$\overrightarrow{OP}$=(a-1,1,2),
设平面A1BD的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{D{A}_{1}}=2x+2z=0}\\{\overrightarrow{n}•\overrightarrow{DB}=2x+2y=0}\end{array}\right.$,
取x=1,得$\overrightarrow{n}$=(1,-1,-1),
∴sinα=|cos<$\overrightarrow{OP},\overrightarrow{n}$>|=|$\frac{\overrightarrow{OP}•\overrightarrow{n}}{|\overrightarrow{OP}|•|\overrightarrow{n}|}$|=|$\frac{a-1-1-2}{\sqrt{(a-1)^{2}+5}•\sqrt{3}}$|=$\frac{\sqrt{3}}{3}•\frac{|a-4|}{\sqrt{(a-1)^{2}+5}}$,
∵0≤a≤2,sinα在a∈[0,2]是减函数,
∴a=2时,sinα取最小值(sinα)min=$\frac{\sqrt{3}}{3}×\frac{|2-4|}{\sqrt{(2-1)^{2}+5}}$=$\frac{\sqrt{2}}{3}$,
a=0时,sinα取最大值(sinα)max=$\frac{\sqrt{3}}{3}×\frac{|0-4|}{\sqrt{(0-1)^{2}+5}}$=$\frac{2\sqrt{2}}{3}$.
∴sinα的取值范围是[$\frac{\sqrt{2}}{3},\frac{2\sqrt{2}}{3}$].
故选:C.
点评 本题考查角的正弦值的取值范围的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{{x}^{4}}$与y=($\sqrt{x}$)4 | B. | y=$\root{3}{{x}^{3}}$与y=$\frac{{x}^{2}}{x}$ | ||
| C. | y=$\sqrt{{x}^{2}+x}$ 与y=$\sqrt{x}$•$\sqrt{x+1}$ | D. | y=$\frac{1}{|x|}$与y=$\frac{1}{\sqrt{{x}^{2}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数$f(x)=\left\{\begin{array}{l}|lgx|,0<x≤10\\-\frac{1}{2}x+6,x>10\end{array}\right.$.
已知函数$f(x)=\left\{\begin{array}{l}|lgx|,0<x≤10\\-\frac{1}{2}x+6,x>10\end{array}\right.$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=1,b=2,c=3 | B. | b=c=1,∠B=45° | C. | a=1,b=2,∠A=100° | D. | a=1,b=$\sqrt{2},∠A={30°}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com