
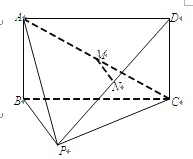
【题目】如图,在四棱锥P-ABCD中,四边形ABCD为矩形,AB⊥BP,M为AC的中点,N为PD上一点.
(1)若MN∥平面ABP,求证:N为PD的中点;
(2)若平面ABP⊥平面APC,求证:PC⊥平面ABP.
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)由线面平行性质定理得MN∥BP,再根据三角形中位线性质得N为PD的中点.(2)过点B作BE⊥AP,则根据面面垂直性质定理得BE⊥平面APC,即BE⊥PC.又易得AB⊥平面BPC,即AB⊥PC,最后根据线面垂直判定定理得PC⊥平面ABP
试题解析:(1)连接BD,由四边形![]() 为矩形得:M为
为矩形得:M为![]() 和
和![]() 的中点,∵MN∥平面ABP,MN平面BPD,平面BPD
的中点,∵MN∥平面ABP,MN平面BPD,平面BPD![]() 平面ABP=BP,∴MN∥BP,∵M为AC的中点,∴N为PD的中点.
平面ABP=BP,∴MN∥BP,∵M为AC的中点,∴N为PD的中点.
(2)在△ABP中,过点B作BE⊥AP于E,∵平面ABP⊥平面APC,平面ABP∩平面APC=AP,BE平面ABP,BE⊥AP
∴BE⊥平面APC, 又PC平面APC,∴BE⊥PC.∵ABCD为矩形,∴ AB⊥BC,又AB⊥BP,BC∩BP=B,BC,BP 平面BPC,∴AB⊥平面BPC, ∴AB⊥PC,又BE⊥PC, AB平面ABP,BE平面ABP,AB∩BE=B, ∴PC⊥平面ABP


科目:高中数学 来源: 题型:
【题目】已知数列{xn}满足x1=1,x2=λ,并且 ![]() =λ
=λ ![]() (λ为非零常数,n=2,3,4,…). (Ⅰ)若x1 , x3 , x5成等比数列,求λ的值;
(λ为非零常数,n=2,3,4,…). (Ⅰ)若x1 , x3 , x5成等比数列,求λ的值;
(Ⅱ)设0<λ<1,常数k∈N* , 证明 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居众显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病倒数计算,下列各选项中,一定符合上述指标的是( )
①平均数 ![]() ;
;
②标准差S≤2;
③平均数 ![]() 且标准差S≤2;
且标准差S≤2;
④平均数 ![]() 且极差小于或等于2;
且极差小于或等于2;
⑤众数等于1且极差小于或等于1.
A.①②
B.③④
C.③④⑤
D.④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:不等式(m-1)x2+(m-1)x+2>0的解集是R,命题q:sin x+cos x>m.如果对于任意的x∈R,命题p是真命题且命题q为假命题,求m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ).
).
(Ⅰ)把曲线![]() 的极坐标方程化为直角坐标方程,并说明曲线
的极坐标方程化为直角坐标方程,并说明曲线![]() 的形状;
的形状;
(Ⅱ)若直线![]() 经过点
经过点![]() ,求直线
,求直线![]() 被曲线
被曲线![]() 截得的线段
截得的线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某造船公司年造船量是20艘,已知造船x艘的产值函数为R(x)=3 700x+45x2-10x3(单位:万元),成本函数为C(x)=460x-5 000(单位:万元).
(1)求利润函数P(x);(提示:利润=产值-成本)
(2)问年造船量安排多少艘时,可使公司造船的年利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com