
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,椭圆上的点
,椭圆上的点![]() 满足
满足![]() ,且
,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() 、
、![]() ,过点
,过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,证明:点
,证明:点![]() 总在直线
总在直线![]() 上.
上.
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,已知曲线![]() ,将曲线
,将曲线![]() 上的点向左平移一个单位,然后纵坐标不变,横坐标轴伸长到原来的2倍,得到曲线
上的点向左平移一个单位,然后纵坐标不变,横坐标轴伸长到原来的2倍,得到曲线![]() ,又已知直线
,又已知直线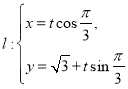 (
(![]() 是参数),且直线
是参数),且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(I)求曲线![]() 的直角坐标方程,并说明它是什么曲线;
的直角坐标方程,并说明它是什么曲线;
(II)设定点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国的高铁技术发展迅速,铁道部门计划在![]() 两城市之间开通高速列车,假设列车在试运行期间,每天在
两城市之间开通高速列车,假设列车在试运行期间,每天在![]() 两个时间段内各发一趟由
两个时间段内各发一趟由![]() 城开往
城开往![]() 城的列车(两车发车情况互不影响),
城的列车(两车发车情况互不影响),![]() 城发车时间及概率如下表所示:
城发车时间及概率如下表所示:
发车 时间 |
|
|
|
|
|
|
概率 |
|
|
|
|
|
|
若甲、乙两位旅客打算从![]() 城到
城到![]() 城,他们到达
城,他们到达![]() 火车站的时间分别是周六的
火车站的时间分别是周六的![]() 和周日的
和周日的![]() (只考虑候车时间,不考虑其他因素).
(只考虑候车时间,不考虑其他因素).
(1)设乙候车所需时间为随机变量![]() (单位:分钟),求
(单位:分钟),求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(2)求甲、乙两人候车时间相等的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() 的顶点为坐标原点O,焦点F在
的顶点为坐标原点O,焦点F在![]() 轴正半轴上,准线
轴正半轴上,准线![]() 与圆
与圆![]() 相切.
相切.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)已知直线![]() 和抛物线
和抛物线![]() 交于点
交于点![]() ,命题
,命题![]() :“若直线
:“若直线![]() 过定点(0,1),则
过定点(0,1),则 ![]() ”,
”,
请判断命题![]() 的真假,并证明.
的真假,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 为常数,
为常数,![]() 的一个零点是
的一个零点是![]() ,函数
,函数![]() 是自然对数的底数, 设函数
是自然对数的底数, 设函数![]() .
.
(1)过点坐标原点![]() 作曲线
作曲线![]() 的切线, 证明切点的横坐标为
的切线, 证明切点的横坐标为![]() ;
;
(2)令![]() ,若函数
,若函数![]() 在区间
在区间![]() 上是单调函数, 求
上是单调函数, 求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ),其最小正周期为
),其最小正周期为![]() .
.
(1)求![]() 在区间
在区间![]() 上的减区间;
上的减区间;
(2)将函数![]() 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向右平移
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,若关于
的图象,若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有且只有一个实数根,求实数
上有且只有一个实数根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com