
【题目】若函数f(x)=tx2-(22t+60)x+144t(x>0).
(1)要使f(x)≥0恒成立,求t的最小值;
(2)令f(x)=0,求使t>20成立的x的取值范围.
【答案】(1)30;(2)(9,16).
【解析】试题分析:(1))因为x2-22x+144>0,所以要使不等式f(x)≥0恒成立,即tx2-(22t+60)x+144t≥0(x>0)恒成立,等价于t≥![]() (x>0)恒成立,求函数最值即可;
(x>0)恒成立,求函数最值即可;
(2)由f(x)=0,得t=![]() ,即可解
,即可解![]() >20即可.
>20即可.
试题解析:
(1)因为x2-22x+144>0,所以要使不等式f(x)≥0恒成立,即tx2-(22t+60)x+144t≥0(x>0)恒成立,等价于t≥![]() (x>0)恒成立,
(x>0)恒成立,
由![]() =
=![]() ≤
≤![]() =30(x>0),
=30(x>0),
当且仅当x=![]() ,即x=12时,等号成立,
,即x=12时,等号成立,
所以当t≥30时,不等式tx2-(22t+60)x+144t≥0恒成立,t的最小值为30.
(2)由t>20,得![]() >20,整理得x2-25x+144<0,即(x-16)(x-9)<0,解得9<x<16,所以使t>20成立的x的取值范围为(9,16).
>20,整理得x2-25x+144<0,即(x-16)(x-9)<0,解得9<x<16,所以使t>20成立的x的取值范围为(9,16).


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以原点O为圆心,椭圆C的长半轴长为半径的圆与直线
,以原点O为圆心,椭圆C的长半轴长为半径的圆与直线![]() 相切.
相切.
⑴求椭圆C的标准方程;
⑵已知点A、B为动直线![]() 与椭圆C的两个交点,问:在x轴上是否存在定点E,使得
与椭圆C的两个交点,问:在x轴上是否存在定点E,使得![]() 为定值?若存在,试求出点E的坐标和定值;若不存在,请说明理由.
为定值?若存在,试求出点E的坐标和定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
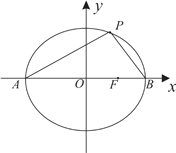
【题目】如图,已知椭圆![]() 的左右顶点分别为
的左右顶点分别为![]() ,右焦点为
,右焦点为![]() ,焦距为
,焦距为![]() ,点
,点![]() 是椭圆C上异于
是椭圆C上异于![]() 两点的动点,
两点的动点, ![]() 的面积最大值为
的面积最大值为![]() .
.
(1)求椭圆C的方程;
(2)若直线![]() 与直线
与直线![]() 交于点
交于点![]() ,试判断以
,试判断以![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系,并作出证明.
的位置关系,并作出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,tanA是以﹣4为第三项,4为第七项的等差数列的公差,tanB是以2为公差,9为第五项的等差数列的第二项,则这个三角形是( )
A.锐角三角形
B.钝角三角形
C.等腰直角三角形
D.等腰或直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
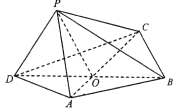
【题目】如图,四边形![]() 中,
中, ![]() 为正三角形,
为正三角形, ![]() ,
, ![]() ,
, ![]() 与
与![]() 中心
中心![]() 点,将
点,将![]() 沿边
沿边![]() 折起,使
折起,使![]() 点至
点至![]() 点,已知
点,已知![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求已知二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 不过原点.
不过原点.
(1)求过点![]() 且与直线
且与直线![]() 垂直的直线的方程;
垂直的直线的方程;
(2)直线![]() 与两坐标轴相交于A、B两点,若直线
与两坐标轴相交于A、B两点,若直线![]() 与点A、B的距离相等,且过原点,求直线
与点A、B的距离相等,且过原点,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一房产商竞标得一块扇形OPQ地皮,其圆心角∠POQ= ![]() ,半径为R=200m,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形ABCD的一边AB在半径OP上,C在圆弧上,D在半径OQ;方案二:矩形EFGH的顶点在圆弧上,顶点G,H分别在两条半径上.请你通过计算,为房产商提供决策建议.
,半径为R=200m,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形ABCD的一边AB在半径OP上,C在圆弧上,D在半径OQ;方案二:矩形EFGH的顶点在圆弧上,顶点G,H分别在两条半径上.请你通过计算,为房产商提供决策建议. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点![]() 分别到两定点
分别到两定点![]()
![]() 连线的斜率之乘积为
连线的斜率之乘积为![]() ,设
,设![]() 的轨迹为曲线
的轨迹为曲线![]() ,
, ![]() ,
, ![]() 分别为曲线
分别为曲线![]() 的左右焦点,则下列命题中:
的左右焦点,则下列命题中:
(1)曲线![]() 的焦点坐标为
的焦点坐标为![]() ,
, ![]() ;
;
(2)若![]() ,则
,则![]()
![]() ;
;
(3)当![]() 时,
时, ![]() 的内切圆圆心在直线
的内切圆圆心在直线![]() 上;
上;
(4)设![]() ,则
,则![]() 的最小值为
的最小值为![]() .
.
其中正确命题的序号是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com