Question

8．求由曲线y=x²与y=2-x²所围成的图形的面积．

Answer 1

分析 作出两个曲线的图象并求出它们的交点坐标．利用定积分公式并结合函数图象的对称性，可得所求面积为函数  2-2x²在区间[0，1]上的定积分值的2倍，再加以运算即可得到本题答案．

解答 解：联立$\left\{{\begin{array}{l}{y={x^2}}\\{y=2-{x^2}}\end{array}}\right.$，…3’
可得交点（-1，1）（1，1），…6’
则面积A=$2\int_0^1{（2-{x^2}-{x^2}）}dx$=$2\int_0^1{（2-2{x^2}）}dx$…9’
=$2[2x-\frac{2}{3}{x^3}]_0^1=2[2•1-\frac{2}{3}{（1）^3}]=4-\frac{4}{3}=\frac{8}{3}$…12’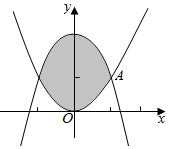

点评 本题求两条曲线围成的曲边图形的面积，着重考查了定积分的几何意义和积分计算公式等知识，属于基础题．