
【题目】在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .设D,E分别为PA,AC中点.
.设D,E分别为PA,AC中点.
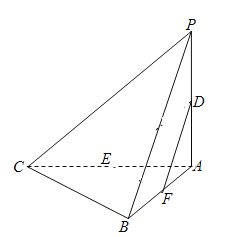
(Ⅰ)求证:![]() 平面PBC;
平面PBC;
(Ⅱ)求证:![]() 平面PAB;
平面PAB;
(Ⅲ)试问在线段AB上是否存在点F,使得过三点D,E,F的平面内的任一条直线都与平面PBC平行?若存在,指出点F的位置并证明;若不存在,请说明理由.
【答案】(Ⅰ)见证明;(Ⅱ)见证明;(Ⅲ)见解析.
【解析】
(Ⅰ)证明以DE∥平面PBC,只需证明DE∥PC;(Ⅱ)证明BC⊥平面PAB,根据线面垂直的判定定理,只需证明PA⊥BC,AB⊥BC;(Ⅲ)当点F是线段AB中点时,证明平面DEF∥平面PBC,可得平面DEF内的任一条直线都与平面PBC平行.
(Ⅰ)证明:因为点E是AC中点,点D为PA的中点,所以![]() .
.
又因为DE![]() 面PBC,PC面PBC,
面PBC,PC面PBC,
所以DE∥平面PBC.
(Ⅱ)证明:因为平面PAC⊥面ABC,平面PAC∩平面ABC=AC,又PA平面PAC,PA⊥AC,
所以PA⊥面ABC,
因为BC平面ABC,
所以PA⊥BC.
又因为AB⊥BC,且PA∩AB=A,
所以BC⊥面PAB.
(Ⅲ)
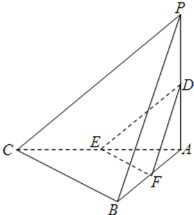
当点F是线段AB中点时,过点D,E,F的平面内的任一条直线都与平面PBC平行.
取AB中点F,连EF,连DF.
由(Ⅰ)可知DE∥平面PBC.
因为点E是AC中点,点F为AB的中点,
所以EF∥BC.
又因为EF![]() 平面PBC,BC平面PBC,
平面PBC,BC平面PBC,
所以EF∥平面PBC.
又因为DE∩EF=E,
所以平面DEF∥平面PBC,
所以平面DEF内的任一条直线都与平面PBC平行.
故当点F是线段AB中点时,过点D,E,F所在平面内的任一条直线都与平面PBC平行.


科目:高中数学 来源: 题型:
【题目】现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率:先由计算器给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7, 8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了 20组随机数:
7527 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该射击运动员射击4次至少击中3次的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方形![]() 的边长为1,点
的边长为1,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,
上,![]() .动点
.动点![]() 从
从![]() 出发沿直线向
出发沿直线向![]() 运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角,当点
运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角,当点![]() 第一次碰到
第一次碰到![]() 时,
时,![]() 与正方形的边碰撞的次数为( )
与正方形的边碰撞的次数为( )
A. 4B. 3C. 8D. 6
查看答案和解析>>
科目:高中数学 来源: 题型:
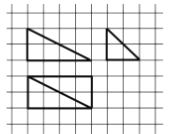
【题目】我国古代数学名著《九章算术·商功》中阐述:“斜解立方,得两壍堵。斜解壍堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”若称为“阳马”的某几何体的三视图如图所示,图中网格纸上小正方形的边长为1,则对该几何体描述:
①四个侧面都是直角三角形;
②最长的侧棱长为![]() ;
;
③四个侧面中有三个侧面是全等的直角三角形;
④外接球的表面积为![]() .
.
其中正确的个数为( )
A. 0B. 1
C. 2D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P与两个定点O(0,0),A(3,0)的距离的比值为2,点P的轨迹为曲线C.
(1)求曲线C的轨迹方程
(2)过点(﹣1,0)作直线与曲线C交于A,B两点,设点M坐标为(4,0),求△ABM面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为圆
为圆![]() 上一动点,圆心
上一动点,圆心![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,点
,点![]() 分别是线段
分别是线段![]() 上的点,且
上的点,且![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 只有一个公共点
只有一个公共点![]() ,且点
,且点![]() 在第二象限,过坐标原点
在第二象限,过坐标原点![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,求
两点,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com