
����Ŀ��Ϊ�˻���֧���۰��������裬�������������ѧ����ҵ���ܵ�����ȥ��ij985��У��֯��һ��ģ����Ƹ����ִӿ��Գɼ��������ȡ100��ѧ���ı��Գɼ��������ɼ��ֳ����飺��1��![]() ����2��
����2��![]() ����3��
����3��![]() ����4��
����4��![]() ����5��
����5��![]() ���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��������ij��ԭ����ֱ��ͼ������������ͬʱ�涨�ɼ�������90��Ϊ�����㡱���ɼ�����90��Ϊ�����á�����ֻ�гɼ������㡱��ѧ�����ܻ��ר������ʸ�.
���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��������ij��ԭ����ֱ��ͼ������������ͬʱ�涨�ɼ�������90��Ϊ�����㡱���ɼ�����90��Ϊ�����á�����ֻ�гɼ������㡱��ѧ�����ܻ��ר������ʸ�.

��1������֪������![]() ��
��![]() ��������Ϊ2:1���벹ȫ��ֱ��ͼ��
��������Ϊ2:1���벹ȫ��ֱ��ͼ��
��2������÷ֲ�����ķ����ӳɼ�Ϊ�����㡱�͡����á���ѡ��10�ˣ������ѡ���ijɼ������㡱�е�һ��������ѡ���ijɼ������㡱��ѧ��������ѡ2�˲μ����ͬ��ר����ԣ�ÿ�˲μ�һ�֣���������ͬ������ױ�ѡ�еĸ���.
���𰸡���1�� ��������2��![]()
��������
��1����Ƶ�ʷֲ�ֱ��ͼ��[90��100]��Ƶ��Ϊ0.3���ɷ�����[90��95����[95��100]��������Ϊ2��1�����������[90��95����[95��100]��Ӧ��С�����и߷ֱ�Ϊ0.02��0.01���ɴ������������ֱ��ͼ��
��2����Ƶ�ʷֲ�ֱ��ͼ��[90��100]��Ƶ��Ϊ0.3���÷ֲ�����ķ����ӳɼ�Ϊ�����㡱�͡����á���ѡ��10�ˣ�����ѡ�С����㡱��ѧ����3�ˣ�ѡ�С����á���ѧ����7�ˣ��ɴ�������ױ�ѡ�еĸ��ʣ�
��1���������������ѧ��������Ϊ100����0.01+0.07+0.06����5=70��,
���� ����ѧ��������Ϊ100-70=30��
����������![]() ��
��![]() ��������Ϊ2:1��
��������Ϊ2:1��
�����������εķ����ֱ�Ϊ20�˺�10��.
�ʲ�����ֱ��ͼ��ͼ��ʾ

��2����Ƶ�ʷֲ�ֱ��ͼ�ã�
[90��100]��Ƶ��Ϊ��1����0.01+0.07+0.06����5��0.3��
���÷ֲ�����ķ����ӳɼ�Ϊ�����㡱�͡����á���ѡ��10�ˣ�
����ѡ�С����㡱��ѧ����3�ˣ�ѡ�С����á���ѧ����7�ˣ�
�����ѡ���ijɼ������㡱�е�һ����
��ѡ���ijɼ������㡱��ѧ��������ѡ2�˲μ����ͬ��ר����ԣ�
�����¼�����n![]() ��
��
�ױ�ѡ�а����Ļ����¼�����m![]() 2��
2��
��ױ�ѡ�еĸ���p![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �������������ʵĺ���
�������������ʵĺ���![]() ��ȫ�壺�ڶ�����
��ȫ�壺�ڶ�����![]() �ڴ���ʵ��
�ڴ���ʵ��![]() ��ʹ��
��ʹ��![]() ����.
����.
��1����֪����![]() ���ж� ����
���ж� ����![]() �Ƿ����ڼ���
�Ƿ����ڼ���![]() ��
��
��2��������![]() ���ڼ���
���ڼ���![]() ������ʵ��
������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3�� ֤������![]() ���ڼ���
���ڼ���![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���д��ڴ�����������100Ԫ�ɲμ�һ�γ齱����������£��˿ͽ�һ���뾶�ʵ���С�������ͼ��ʾ���������Ϸ����˿ڴ���С�����������µĹ����У���3��������ɫ�ϰ���������A����B���У��˿���Ӧ��ô�����Ľ�Ʒ.��֪С��ÿ��������ɫ�ϰ���ʱ��������������ĸ��ʶ�Ϊ![]() .�������С���ڸó��й�������108Ԫ�����ջ�������ɲμ�һ�γ齱����С�����A���еĽ�Ʒ�ĸ���Ϊ_____.
.�������С���ڸó��й�������108Ԫ�����ջ�������ɲμ�һ�γ齱����С�����A���еĽ�Ʒ�ĸ���Ϊ_____.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ��һ������������һ����������������������������������ϣ���һ�������������ĵ����ϣ����������ĸ�Ϊ15������߳�Ϊ12���ڽ����������IJ����Ϊ120.
��һ������������һ����������������������������������ϣ���һ�������������ĵ����ϣ����������ĸ�Ϊ15������߳�Ϊ12���ڽ����������IJ����Ϊ120.
��1�����������ĸߣ�
��2�����������ϵ���������õ�С����ԭ���IJ����֮��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƹ�������涨��һ�ֱ�����˫���ȷ���10ƽǰ��һ����������2�κԷ�����������2�Σ������ֻ���ÿ�η���ʤ����1�֣�������0�֡����ڼס��ҵı����У�ÿ�η������1�ֵĸ���Ϊ![]() ���ҷ����1�ֵĸ���Ϊ
���ҷ����1�ֵĸ���Ϊ![]() �����η����ʤ�������������ס��ҵ�һ�ֱ����У����ȷ���.��ʼ��4�η���ʱ���ס��ҵıȷ�Ϊ1��2�ĸ���Ϊ________.
�����η����ʤ�������������ס��ҵ�һ�ֱ����У����ȷ���.��ʼ��4�η���ʱ���ס��ҵıȷ�Ϊ1��2�ĸ���Ϊ________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,������![]() ��,����ABCD��ֱ������,
��,����ABCD��ֱ������,![]() ,
,![]() ��
��![]() ,����
,����![]() ƽ��ABCD,��
ƽ��ABCD,��![]() .
.
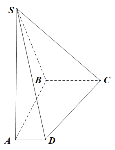
��1����֤:ƽ��![]() ƽ��
ƽ��![]() ;
;
��2����ƽ��![]() ��ƽ��
��ƽ��![]() ���ɶ���ǵ�����ֵ.
���ɶ���ǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ڹ۲�õ����ڽ�ͨ��æ��ʱ���ڣ�ij��·�����ij�����![]() ��ǧ��/h����������ƽ���ٶ�
��ǧ��/h����������ƽ���ٶ�![]() ֮��ĺ�����ϵʽΪ��
֮��ĺ�����ϵʽΪ��![]() ��
��
��1����Ҫ���ڸö�ʱ���ڳ���������2ǧ��![]() ����������ƽ���ٶ�Ӧ��ʲô��Χ�ڣ�
����������ƽ���ٶ�Ӧ��ʲô��Χ�ڣ�
��2���ڸ�ʱ���ڣ����涨����ƽ���ٶȲ��ó���![]() ����������ƽ���ٶ�
����������ƽ���ٶ�![]() Ϊ����ʱ������������������Ϊ���٣�
Ϊ����ʱ������������������Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����![]() ����
����![]() ��
��![]() Ϊ�������Բ
Ϊ�������Բ![]() ��.
��.
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2������![]() ��ֱ��
��ֱ��![]() ��
��![]() ������
������![]() ����
����![]() ����
����![]() �㣬��
�㣬��![]() ��
��![]() ����
����![]() ����
����![]() ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���(a��c��cos B)��sin B��(b��c��cos A)��sin A���жϡ�ABC����״��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com