
【题目】如图,在三棱锥![]() 中,
中,![]() 底面
底面![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.
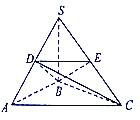
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的大小.
的平面角的大小.
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,直线
,直线![]() 不过原点
不过原点![]() 且不平行于坐标轴,
且不平行于坐标轴,![]() 与
与![]() 有两个交点
有两个交点![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() .证明:
.证明:
(![]() )直线
)直线![]() 的斜率与
的斜率与![]() 的斜率的乘积为定值
的斜率的乘积为定值![]() .
.
(![]() )若
)若![]() 过点
过点![]() ,延长线段
,延长线段![]() 与
与![]() 交于点
交于点![]() ,当四边形
,当四边形![]() 为平行四边形时,则直线
为平行四边形时,则直线![]() 的斜率
的斜率![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水,天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸,若盆中积水深九寸,则平地降雨量是(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸)( )
A.2寸B.3寸C.4寸D.5寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)求与椭圆![]() 有共同焦点且过点
有共同焦点且过点![]() 的双曲线的标准方程;
的双曲线的标准方程;
(2)已知抛物线的焦点在![]() 轴上,抛物线上的点
轴上,抛物线上的点![]() 到焦点的距离等于5,求抛物线的标准方程和
到焦点的距离等于5,求抛物线的标准方程和![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学为了解本校某年级女生的身高情况,从本校该年级的女学生中随机选出100名并统计她们的身高(单位:cm),得到的频数分布表如下:
分组 |
|
|
|
|
频数 | 20 | 20 | 50 | 10 |
(1)用分层抽样的方法从身高在![]() 和
和![]() 的女生中共抽取6人,则身高在
的女生中共抽取6人,则身高在![]() 内的女生应抽取几人?
内的女生应抽取几人?
(2)在(1)中抽取的6人中,再随机抽取2人,求这2人身高都在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为正方形,平面
中,底面ABCD为正方形,平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,E,F分别为AD,PB的中点.
,E,F分别为AD,PB的中点.
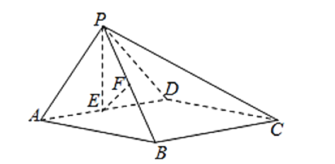
(1)求证:![]() 平面ABCD;
平面ABCD;
(2)求证:![]() 平面PCD;
平面PCD;
(3)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
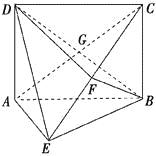
【题目】如图所示,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥平面BCE;
(2)求证:AE∥平面BFD;
(3)求三棱锥C-BGF的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com