
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为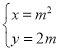 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(Ⅱ)已知点![]() 设直线
设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】(导学号:05856310)
已知函数f(x)=x+![]() +ln x(a∈R).
+ln x(a∈R).
(Ⅰ)当a=2时, 求函数f(x)的单调区间;
(Ⅱ)若关于x的函数g(x)=![]() -f(x)+ln x+2e(e为自然对数的底数)有且只有一个零点,求实数a的值.
-f(x)+ln x+2e(e为自然对数的底数)有且只有一个零点,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列![]() 的前
的前![]() 项中的最大项为
项中的最大项为![]() ,最小项为
,最小项为![]() ,设
,设![]()
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若数列![]() 是等差数列,求证:数列
是等差数列,求证:数列![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,直线
轴的正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值与最小值.
的距离的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代名著《张丘建算经》中记载:“今有方锥下广二丈,高三丈,欲斩末为方亭;令上方六尺:问亭方几何?”大致意思是:有一个四棱锥下底边长为二丈,高三丈;现从上面截取一段,使之成为正四棱台状方亭,且四棱台的上底边长为六尺,则该正四棱台的高为________尺,体积是_______立方尺(注:1丈=10尺).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区高考实行新方案,规定:语文、数学和英语是学生的必考科目,学生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目.若一个学生从六个科目中选出了三个科目作为选考科目,则称该学生确定选考方案,否则称该学生待确定选考方案.例如学生甲选择“物理、化学和生物”三个选考科目,则称学生甲确定选考方案.某校为了解高一年级![]() 名学生选考科目的意向,随机选取
名学生选考科目的意向,随机选取![]() 名学生进行了一次调查,统计情况如下表:
名学生进行了一次调查,统计情况如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男 生 | 选考方案确定的有 |
|
|
|
|
|
|
选考方案待确定的有 |
|
|
|
|
|
| |
女 生 | 选考方案确定的有 |
|
|
|
|
|
|
选考方案待确定的有 |
|
|
|
|
|
|
(1)估计该校高一年级已确定选考方案的学生有多少人?
(2)假设男生、女生选择选考科目是相互独立的.从确定选考方案的![]() 名男生中随机选出
名男生中随机选出![]() 名,从确定选考方案的
名,从确定选考方案的![]() 名女生中随机选出
名女生中随机选出![]() 名,试求该男生和该女生的选考方案中都含有历史科目的概率;
名,试求该男生和该女生的选考方案中都含有历史科目的概率;
(3)从确定选考方案的8名男生中随机选出2名,设随机变量![]() 表示
表示![]() 名男生选考方案相同,
名男生选考方案相同,![]() 表示
表示![]() 名男生选考方案不同,求
名男生选考方案不同,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com