

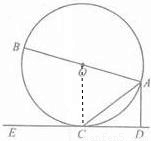
 证明:(Ⅰ)连接OC,如下图所示:
证明:(Ⅰ)连接OC,如下图所示: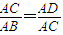 ,
,

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
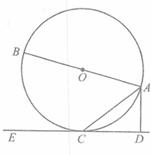 选做题
选做题查看答案和解析>>
科目:高中数学 来源:2013届陕西省师大附中高三第四次模拟考试理科数学试卷(带解析) 题型:填空题
A.(不等式选做题)若不存在实数 使
使 成立,则实数
成立,则实数 的取值集合是__________.
的取值集合是__________.
B. (几何证明选做题) )如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于点D.过点C作BD的平行线与圆相交于点E,与AB相交于点F,AF=3,FB=1,EF= ,则线段CD的长为________.
,则线段CD的长为________.
C. (坐标系与参数方程选做题) 已知直线 :
: (t为参数)与圆C2:
(t为参数)与圆C2: (
( 为参数)的位置关系不可能是________.
为参数)的位置关系不可能是________.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年陕西省高三第四次模拟考试理科数学试卷(解析版) 题型:填空题
A.(不等式选做题)若不存在实数 使
使 成立,则实数
成立,则实数 的取值集合是__________.
的取值集合是__________.
B. (几何证明选做题) )如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于点D.过点C作BD的平行线与圆相交于点E,与AB相交于点F,AF=3,FB=1,EF= ,则线段CD的长为________.
,则线段CD的长为________.

C. (坐标系与参数方程选做题) 已知直线 :
: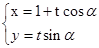 (t为参数)与圆C2:
(t为参数)与圆C2: (
( 为参数)的位置关系不可能是________.
为参数)的位置关系不可能是________.
查看答案和解析>>
科目:高中数学 来源:2012年吉林省高考数学仿真模拟试卷8(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com