
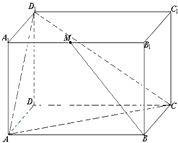
 如图所示,已知长方体ABCD-A1B1C1D1中,AD=3,AB=AA1=4,M是A1B1的中点.
如图所示,已知长方体ABCD-A1B1C1D1中,AD=3,AB=AA1=4,M是A1B1的中点.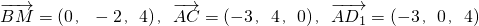 .
.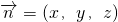 ,则
,则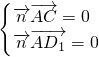 ,即
,即 .取z=3,得x=4,y=3.
.取z=3,得x=4,y=3.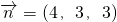 .
. ,
,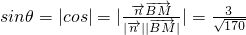 ,
, .
. .
.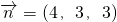 ,
, ,
,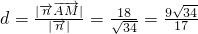 .
.  .
. 的坐标和平面ACD1的法向量
的坐标和平面ACD1的法向量 ,最后求
,最后求 与
与 的夹角的余弦值,取绝对值后即为线面角的正弦值
的夹角的余弦值,取绝对值后即为线面角的正弦值 ,再求向量
,再求向量 的坐标,最后求
的坐标,最后求 在
在 方向上的投影的长度即为M到平面ACD1的距离
方向上的投影的长度即为M到平面ACD1的距离

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
 (2006•静安区二模)如图所示,已知长方体ABCD-A1B1C1D1中,AC与BD交于E点,且AB=AD=2,两条异面直线A1D与AC所成的角的大小为arccos
(2006•静安区二模)如图所示,已知长方体ABCD-A1B1C1D1中,AC与BD交于E点,且AB=AD=2,两条异面直线A1D与AC所成的角的大小为arccos
| ||
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
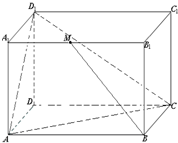 (2009•黄浦区一模)如图所示,已知长方体ABCD-A1B1C1D1中,AD=3,AB=AA1=4,M是A1B1的中点.
(2009•黄浦区一模)如图所示,已知长方体ABCD-A1B1C1D1中,AD=3,AB=AA1=4,M是A1B1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
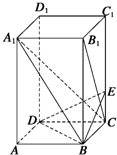 如图所示,已知长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,E是棱CC1上的点,且CE=1.
如图所示,已知长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,E是棱CC1上的点,且CE=1.查看答案和解析>>
科目:高中数学 来源: 题型:
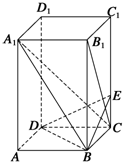 如图所示,已知长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,E是棱CC1上的点,且BE⊥B1C.
如图所示,已知长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,E是棱CC1上的点,且BE⊥B1C.查看答案和解析>>
科目:高中数学 来源:2013届江苏省扬州市邗江区高二下学期期中考试数学试卷(解析版) 题型:解答题
如图所示,已知长方体 中,
中,
 ,
, 是棱
是棱 上的点,且
上的点,且 。
。

(1)求 的长;
的长;
(2)求证: 平面
平面 ;
;
(3)求 与平面
与平面 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com