
【题目】已知函数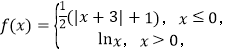 若存在实数
若存在实数![]() ,满足
,满足![]() ,则
,则![]() 的最大值是____.
的最大值是____.
【答案】![]() .
.
【解析】分析: 根据函数f(x)图象判断a,b,c关系即范围,用c表示出af(a)+bf(b)+cf(c),根据函数单调性求出最大值.
详解: 作出f(x)的函数图象如图所示:
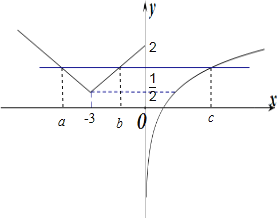
∵存在实数a<b<c,满足f(a)=f(b)=f(c),
∴a+b=﹣6,
∴af(a)+bf(b)+cf(c)=(a+b+c)f(c)=(c﹣6)lnc,
由函数图象可知:![]() <c<e2,
<c<e2,
设g(c)=(c﹣6)lnc,则![]() =lnc+1﹣
=lnc+1﹣![]() ,
,
显然![]() 在(
在(![]() ,e2]上单调递增,
,e2]上单调递增,
∵![]() =2﹣
=2﹣![]() <0,
<0,![]() =3﹣
=3﹣![]() >0,
>0,
∴![]() 在(
在(![]() ,e2]上存在唯一一个零点,不妨设为c0,
,e2]上存在唯一一个零点,不妨设为c0,
在g(c)在(![]() ,c0)上单调递减,在(c0,e2]上单调递增,
,c0)上单调递减,在(c0,e2]上单调递增,
又g(![]() )=
)=![]() (
(![]() ﹣6)<0,g(e2)=2(e2﹣6)>0,
﹣6)<0,g(e2)=2(e2﹣6)>0,
∴g(c)的最大值为g(e2)=2e2﹣12.
故答案为:2e2﹣12
点睛: (1)本题有三个关键点,其一是能够很熟练准确地画出函数的图像;其二是从图像里能发现a+b=-6, ![]() <c<e2;其三是能够想到构造函数g(c)=(c﹣6)lnc,利用导数求函数的最大值.(2)本题要求函数的图像和性质掌握的比较好,属于中档题.
<c<e2;其三是能够想到构造函数g(c)=(c﹣6)lnc,利用导数求函数的最大值.(2)本题要求函数的图像和性质掌握的比较好,属于中档题.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】在全球关注的抗击“新冠肺炎”中,某跨国科研中心的一个团队,研制了甲、乙两种治疗“新冠肺炎”新药,希望知道哪种新药更有效,为此进行动物试验,试验方案如下:
第一种:选取![]() 共10只患病白鼠,服用甲药后某项指标分别为:
共10只患病白鼠,服用甲药后某项指标分别为:![]() ;
;
第二种:选取![]() 共10只患病白鼠,服用乙药后某项指标分别为:
共10只患病白鼠,服用乙药后某项指标分别为:![]() ;
;
该团队判定患病白鼠服药后这项指标不低于85的确认为药物有效,否则确认为药物无效.
(1)已知第一种试验方案的10个数据的平均数为89,求这组数据的方差;
(2)现需要从已服用乙药的10只白鼠中随机抽取7只,记其中服药有效的只数为![]() ,求
,求![]() 的分布列与期望;
的分布列与期望;
(3)该团队的另一实验室有1000只白鼠,其中900只为正常白鼠,100只为患病白鼠,每用新研制的甲药给所有患病白鼠服用一次,患病白鼠中有![]() 变为正常白鼠,但正常白鼠仍有
变为正常白鼠,但正常白鼠仍有![]() 变为患病白鼠,假设实验室的所有白鼠都活着且数量不变,且记服用
变为患病白鼠,假设实验室的所有白鼠都活着且数量不变,且记服用![]() 次甲药后此实验室正常白鼠的只数为
次甲药后此实验室正常白鼠的只数为![]() .
.
(i)求![]() 并写出
并写出![]() 与
与![]() 的关系式;
的关系式;
(ii)要使服用甲药两次后,该实验室正常白鼠至少有950只,求最大的正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,设圆
,设圆![]() 与圆
与圆![]() 的公共弦所在直线为
的公共弦所在直线为![]() .
.
(1)求直线![]() 的极坐标方程;
的极坐标方程;
(2)若以坐标原点为中心,直线![]() 顺时针方向旋转
顺时针方向旋转![]() 后与圆
后与圆![]() 、圆
、圆![]() 分别在第一象限交于
分别在第一象限交于![]() 、
、![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某面包推出一款新面包,每个面包的成本价为4元,售价为10元,该款面包当天只出一炉(一炉至少15个,至多30个),当天如果没有售完,剩余的面包以每个2元的价格处理掉,为了确定这一炉面包的个数,该店记录了这款新面包最近30天的日需求量(单位:个),整理得下表:

(1)根据表中数据可知,频数![]() 与日需求量
与日需求量![]() (单位:个)线性相关,求
(单位:个)线性相关,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)以30天记录的各日需求量的频率代替各日需求量的概率,若该店这款新面包出炉的个数为24,记当日这款新面包获得的总利润为![]() (单位:元).
(单位:元).
(ⅰ)若日需求量为15个,求![]() ;
;
(ⅱ)求![]() 的分布列及其数学期望.
的分布列及其数学期望.
相关公式: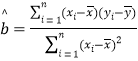
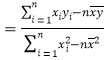 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次考试,班主任从全班同学中随机抽取一个容量为8的样本,他们的数学物理分数对应如下表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学分数 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
物理分数 | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
绘出散点图如下:

根据以上信息,判断下列结论:
①根据此散点图,可以判断数学成绩与物理成绩具有线性相关关系;
②根据此散点图,可以判断数学成绩与物理成绩具有一次函数关系;
③甲同学数学考了80分,那么,他的物理成绩一定比数学只考了60分的乙同学的物理成绩要高.
其中正确的个数为( ).
A.0B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设![]() 为曲线
为曲线![]() 上的点,
上的点,![]() ,垂足为
,垂足为![]() ,若
,若![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.
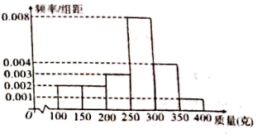
(1)经计算估计这组数据的中位数;
(2)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在
的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在![]() 内的概率.
内的概率.
(3)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有10000个,经销商提出如下两种收购方案:
A:所有芒果以10元/千克收购;
B:对质量低于250克的芒果以2元/个收购,高于或等于250克的以3元/个收购,通过计算确定种植园选择哪种方案获利更多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点![]() 为极点,x轴的正半轴为极轴,建立坐标系,两个坐标系取相同的单位长度.已知直线
为极点,x轴的正半轴为极轴,建立坐标系,两个坐标系取相同的单位长度.已知直线![]() 的参数方程为
的参数方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线![]() 的直角坐标方程
的直角坐标方程
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,
两点,![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com