
分析 (Ⅰ)利用A(-3,0),B(1,0),线段AB是圆M的直径,则圆心M的坐标为(-1,0),又因为|AM|=2,即可求圆M的方程;
(Ⅱ)过点(0,2)的直线l与圆M相交于D,E两点,且$|{DE}|=2\sqrt{3}$,分类讨论,即可求直线l的方程.
解答 解:(Ⅰ)已知点A(-3,0),B(1,0),线段AB是圆M的直径,
则圆心M的坐标为(-1,0).--------------------------(2分)
又因为|AM|=2,--------------------------(3分)
所以圆M的方程为(x+1)2+y2=4.-------------------------(4分)
(Ⅱ)由(Ⅰ)可知圆M的圆心M(-1,0),半径为2.
设N为DE中点,则MN⊥l,$|DN|\;=\;|EN|=\frac{1}{2}•2\sqrt{3}=\sqrt{3}$,-------------------------(5分)
则$|MN|\;=\sqrt{4-{{(\sqrt{3})}^2}}=1$.--------------------------(6分)
当l的斜率不存在时,l的方程为x=0,此时|MN|=1,符合题意;-------------------------(7分)
当l的斜率存在时,设l的方程为y=kx+2,由题意得$\frac{|k(-1)+2|}{{\sqrt{{k^2}+1}}}=1$--------------------------(8分)
解得$k=\frac{3}{4}$,--------------------------(9分)
故直线l的方程为$y=\frac{3}{4}x+2$,即3x-4y+8=0.--------------------------(10分)
综上,直线l的方程为x=0或3x-4y+8=0.
点评 本题考查圆的方程,考查直线与圆的位置关系,考查分类讨论的数学思想,属于中档题.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:解答题
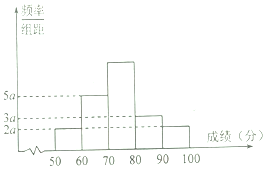 某学习小组20名学生一次数学考试成绩(单位:分)频率直方图如图所示,已知前三个矩形框垂直于横轴的高度成等差数列.
某学习小组20名学生一次数学考试成绩(单位:分)频率直方图如图所示,已知前三个矩形框垂直于横轴的高度成等差数列.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{5}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com