
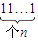
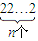
 (10n-1)•10n+
(10n-1)•10n+ (10n-1)=(
(10n-1)=(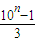 )(
)(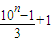 )
)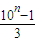 为整数,从而可得(
为整数,从而可得(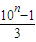 )(
)(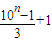 )为整数.
)为整数. ×102n+
×102n+ ×10n-
×10n- ,利用分组求和,分别利用等比数列、等差数列的求和公式即可
,利用分组求和,分别利用等比数列、等差数列的求和公式即可 (10n-1)•10n+
(10n-1)•10n+ (10n-1)(2分)
(10n-1)(2分) (10n-1)(10n+2)=(
(10n-1)(10n+2)=(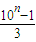 )(
)(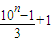 )(4分)
)(4分)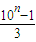 ,则A=
,则A=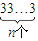 为整数
为整数 102n+
102n+ 10n-
10n- (8分)
(8分) (102+104+…+102n)+
(102+104+…+102n)+ (10+102+…+10n)-
(10+102+…+10n)- n
n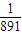 (102n+2)+11•10n+1-198n-210(12分)
(102n+2)+11•10n+1-198n-210(12分)

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
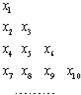 若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足xnan=xn+1an+1=xn+2an+2(n∈N*).
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足xnan=xn+1an+1=xn+2an+2(n∈N*).| n |
| 2 |
| 1 |
| 3 |
| x1-1 |
| x2-1 |
| x2-1 |
| x3-1 |
| xn-1 |
| xn+1-1 |
| n |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源:2009-2010学年浙江省台州市高一(下)期末数学试卷(解析版) 题型:选择题
查看答案和解析>>
科目:高中数学 来源:2011年湖南省益阳市沅江市高三质量检测数学试卷1(理科)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com