
已知圆O: ,点O为坐标原点,一条直线
,点O为坐标原点,一条直线 :
: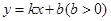 与圆O相切并与椭圆
与圆O相切并与椭圆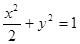 交于不同的两点A、B
交于不同的两点A、B
(1)设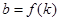 ,求
,求 的表达式;
的表达式;
(2)若 ,求直线
,求直线 的方程;
的方程;
(3)若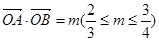 ,求三角形OAB面积的取值范围.
,求三角形OAB面积的取值范围.
科目:高中数学 来源:2007-2008学年湖北省襄阳市枣阳一中、随州市曾都一中高二(上)期中数学试卷(文理合卷)(解析版) 题型:解答题
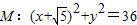 ,定点
,定点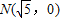 ,点P为圆M上的动点,点Q在NP上,点G在MP上,且满足
,点P为圆M上的动点,点Q在NP上,点G在MP上,且满足 .
. ,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.查看答案和解析>>
科目:高中数学 来源:2010学年吉林省长春市东北师大附中高考数学五模试卷(文科)(解析版) 题型:解答题
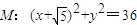 ,定点
,定点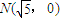 ,点P为圆M上的动点,点Q在NP上,点G在MP上,且满足
,点P为圆M上的动点,点Q在NP上,点G在MP上,且满足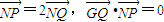 .
.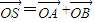 ,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.查看答案和解析>>
科目:高中数学 来源:2011年甘肃省兰州一中高考实战演练数学试卷4(理科)(解析版) 题型:解答题
 ,定点
,定点 ,点P为圆M上的动点,点Q在NP上,点G在MP上,且满足
,点P为圆M上的动点,点Q在NP上,点G在MP上,且满足 .
. ,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.查看答案和解析>>
科目:高中数学 来源:2012年广东省汕头市高考数学二模试卷(理科)(解析版) 题型:解答题
 ,定点
,定点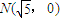 ,点P为圆M上的动点,点Q在NP上,点G在MP上,且满足
,点P为圆M上的动点,点Q在NP上,点G在MP上,且满足 .
. ,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.查看答案和解析>>
科目:高中数学 来源:2009年高考数学压轴试卷集锦(2)(解析版) 题型:解答题
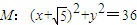 ,定点
,定点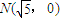 ,点P为圆M上的动点,点Q在NP上,点G在MP上,且满足
,点P为圆M上的动点,点Q在NP上,点G在MP上,且满足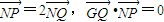 .
.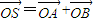 ,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com