
【题目】.已知函数f(x)=x2-2x-3,若x∈[t,t+2]时,求函数f(x)的最值.
【答案】详见解析.
【解析】试题分析:二次函数的对称轴是x=1,分类讨论对称轴在区间左边,对称轴在区间右边以及对称轴在区间内三类讨论,按照函数的单调性求出最值,当对称轴在区间内时,再分成对称轴在区间中点左边和右边两类求最大值,最后写成分段函数的形式.
试题解析:
∵对称轴x=1,
(1)当1≥t+2,即t≤-1时,f(x)max=f(t)=t2-2t-3,f(x)min=f(t+2)=t2+2t-3.
(2)当![]() ≤1<t+2,即-1<t≤0时,f(x)max=f(t)=t2-2t-3,f(x)min=f(1)=-4.
≤1<t+2,即-1<t≤0时,f(x)max=f(t)=t2-2t-3,f(x)min=f(1)=-4.
(3)当t≤1<![]() ,即0<t≤1时,f(x)max=f(t+2)=t2+2t-3,f(x)min=f(1)=-4.
,即0<t≤1时,f(x)max=f(t+2)=t2+2t-3,f(x)min=f(1)=-4.
(4)当1<t,即t>1时,f(x)max=f(t+2)=t2+2t-3,f(x)min=f(t)=t2-2t-3.
设函数最大值为g(t),最小值为φ(t)时,则有
g(t)=![]() φ(t)=
φ(t)=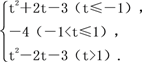
点睛:本题考查二次函数的最值问题,体现了分类讨论思想,属于中档题.由题意二次函数的开口向上,且对称轴为x=1,故讨论对称轴与区间端点t和t+2的大小关系,当对称轴大于等于t+2时,函数单调递减;当对称轴小于t时,函数单调递增;当对称轴在区间内时,函数先减后增,在对称轴处取最小值,再比较1与两端点中点的大小,当1大于等于中点时,在x=t处取最大值, 当1小于中点时,在x=t+2处取最大值.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
【题目】用长为18 m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
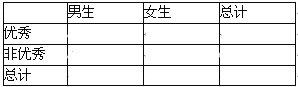
【题目】在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下:
表1:男生
![]()
表2:女生
![]()
(1)从表二的非优秀学生中随机选取2人交谈,求所选2人中恰有1人测评等级为合格的概率;
(2)由表中统计数据填写下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
参考数据与公式:
K2=![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
临界值表:
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如下表所示:
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性不高 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中有1名男生的概率是多少?
(3)学生的学习积极性与对待班极工作的态度是否有关系?请说明理由.
附:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
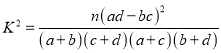
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x),当x,y∈R时,恒有f(x+y)=f(x)+f(y).当x>0时,f(x)>0.
(1)求证:f(x)是奇函数;
(2)若f(1)=![]() ,试求f(x)在区间[-2,6]上的最值.
,试求f(x)在区间[-2,6]上的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数: 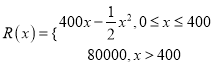 ,其中
,其中![]() 是仪器的月产量
是仪器的月产量
(1)将利润![]() 表示为月产量
表示为月产量![]() 的函数
的函数
(2)当月产量![]() 为何值时,公司所获利润最大?最大利润是多少元?(总收益=总成本+利润)
为何值时,公司所获利润最大?最大利润是多少元?(总收益=总成本+利润)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a-![]() (a∈R).
(a∈R).
(1) 判断函数f(x)的单调性并给出证明;
(2) 若存在实数a使函数f(x)是奇函数,求a;
(3)对于(2)中的a,若f(x)≥![]() ,当x∈[2,3]时恒成立,求m的最大值.
,当x∈[2,3]时恒成立,求m的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com