
【题目】已知函数f(x)=|2x-a|+|2x-1|(a∈R).
(1)当a=-1时,求f(x)≤2的解集;
(2)若f(x)≤|2x+1|的解集包含集合![]() ,求实数a的取值范围.
,求实数a的取值范围.
【答案】(1) ![]() ;(2)0≤a≤3.
;(2)0≤a≤3.
【解析】试题分析:
(1)代入![]() ,由
,由![]() ,根据绝对值的几何意义,求出满足条件的
,根据绝对值的几何意义,求出满足条件的![]() 的值即可;
的值即可;
(2)根据题意,把![]() ,转化为
,转化为![]() 在
在![]() 上恒成立,求解
上恒成立,求解![]() ,即可求解实数
,即可求解实数![]() 的取值范围.
的取值范围.
试题解析:
(1)当a=-1时,f(x)=|2x+1|+|2x-1|,f(x)≤2![]() +
+![]() ≤1,
≤1,
上述不等式的几何意义为数轴上点x到两点-![]() ,
,![]() 距离之和小于或等于1,则-
距离之和小于或等于1,则-![]() ≤x≤
≤x≤![]() ,
,
即原不等式的解集为![]() .
.
(2)∵f(x)≤|2x+1|的解集包含![]() ,
,
∴当x∈![]() 时,不等式f(x)≤|2x+1|恒成立,
时,不等式f(x)≤|2x+1|恒成立,
∴当x∈![]() 时,|2x-a|+2x-1≤2x+1恒成立,
时,|2x-a|+2x-1≤2x+1恒成立,
∴2x-2≤a≤2x+2在x∈![]() 上恒成立,
上恒成立,
∴(2x-2)max≤a≤(2x+2)min![]() ,∴0≤a≤3.
,∴0≤a≤3.


 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆G: ![]() 的离心率为
的离心率为![]() ,过椭圆G右焦点F的直线m:x=1与椭圆G交于点M(点M在第一象限).
,过椭圆G右焦点F的直线m:x=1与椭圆G交于点M(点M在第一象限).
(Ⅰ)求椭圆G的方程;
(Ⅱ)已知A为椭圆G的左顶点,平行于AM的直线l与椭圆G相交于B,C两点,请判断直线MB,MC是否关于直线m对称,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线E: ![]() (a>0,b>0)的渐近线方程为3x±4y=0,且过焦点垂直x轴的直线与双曲线E相交弦长为
(a>0,b>0)的渐近线方程为3x±4y=0,且过焦点垂直x轴的直线与双曲线E相交弦长为![]() ,过双曲线E中心的直线与双曲线E交于A,B两点,在双曲线E上取一点C(与A,B不重合),直线AC,BC 的斜率分别为k1,k2,则k1k2等于( )
,过双曲线E中心的直线与双曲线E交于A,B两点,在双曲线E上取一点C(与A,B不重合),直线AC,BC 的斜率分别为k1,k2,则k1k2等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某销售公司为了解员工的月工资水平,从1000位员工中随机抽取100位员工进行调查,得到如下的频率分布直方图:
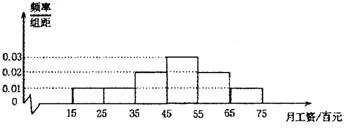
(1)试由此图估计该公司员工的月平均工资;
(2)该公司工资发放是以员工的营销水平为重要依据来确定的,一般认为,工资低于4500。元的员工属于学徒阶段,没有营销经验,若进行营销将会失败;高于4500元的员工是具备营销成熟员工,基进行营销将会成功。现将该样本按照“学徒阶段工资”、“成熟员工工资”分成两层,进行分层抽样,从中抽出5人,在这5人中任选2人进行营销活动。活动中,每位员工若营销成功,将为公司赢得3万元,否则公司将损失1万元。试问在此次比赛中公司收入多少万元的可能性最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面五边形ABCDE中,AB∥CE,且AE=2,∠AEC=60°,CD=ED=![]() ,cos∠EDC=
,cos∠EDC=![]() .将△CDE沿CE折起,使点D移动到P的位置,且AP=
.将△CDE沿CE折起,使点D移动到P的位置,且AP=![]() ,得到四棱锥P-ABCE.
,得到四棱锥P-ABCE.
(1)求证:AP⊥平面ABCE;
(2)记平面PAB与平面PCE相交于直线l,求证:AB∥l.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x-1|+|x-a|,a∈R.
(Ⅰ)当a=4时,求不等式f(x)≥7的解集;
(Ⅱ)若f(x)≥5对x∈R恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点.

(Ⅰ)求证:PC∥平面EBD;
(Ⅱ)求证:平面PBC⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856284)
在△ABC中,角A,B,C的对边分别为a,b,c,已知c=b(1+2cosA).
(Ⅰ)求证:A=2B;
(Ⅱ)若a=![]() ,B=
,B=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com