
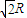 ,AB,CD是互相垂直的直径,沿AB将圆面折成大小为θ的二面角.
,AB,CD是互相垂直的直径,沿AB将圆面折成大小为θ的二面角.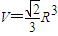 ?
?
 ,先由此体积求出D到底面的距离,然后再求二面角的大小.
,先由此体积求出D到底面的距离,然后再求二面角的大小. 解:(I)由已知,易得AC=CB=BD=DA=2R,
解:(I)由已知,易得AC=CB=BD=DA=2R,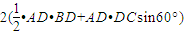

 ;
; ,
,



 ,
, ,
, 时,解得
时,解得 ,所以θ=30°或150°.
,所以θ=30°或150°.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:高中数学 来源: 题型:
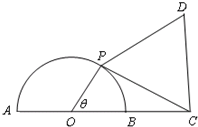 如图,已知⊙O的半径为1,点C在直径AB的延长线上,BC=1,点P是半圆上的一个动点,以PC为边作正三角形PCD,且点D与圆心分别在PC两侧.
如图,已知⊙O的半径为1,点C在直径AB的延长线上,BC=1,点P是半圆上的一个动点,以PC为边作正三角形PCD,且点D与圆心分别在PC两侧.查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
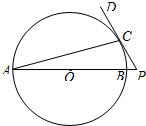 (2011•西城区二模)如图,AB是圆O的直径,P在AB的延长线上,PD切圆O于点C.已知圆O半径为
(2011•西城区二模)如图,AB是圆O的直径,P在AB的延长线上,PD切圆O于点C.已知圆O半径为| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
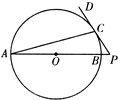 (1)如图,AB是圆O的直径,P在AB的延长线上,PD切圆O于点C.已知圆O半径为y=x-1(1≤x≤2),OP=2,则PC=
(1)如图,AB是圆O的直径,P在AB的延长线上,PD切圆O于点C.已知圆O半径为y=x-1(1≤x≤2),OP=2,则PC=| π | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com