
已知函数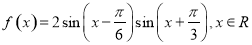 .
.
(1)求函数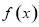 的最小正周期;
的最小正周期;
(2)在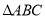 中,若
中,若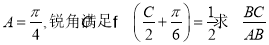 的值.
的值.
科目:高中数学 来源:2013-2014学年山东省济南市高三3月考模拟考试理科数学试卷(解析版) 题型:选择题
已知集合A={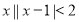 },B={
},B={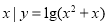 },设U=R,则A
},设U=R,则A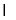 (
(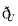 B)等于( )
B)等于( )
(A) [3,+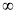 ) (B) (-1,0]
) (B) (-1,0]
(C) (3,+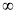 ) (D) [-1,0]
) (D) [-1,0]
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省日照市高三5月统一质量检测考试理科数学试卷(解析版) 题型:选择题
设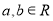 ,则“
,则“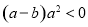 ”是“
”是“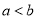 ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省日照市高三5月统一质量检测考试文科数学试卷(解析版) 题型:选择题
角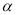 顶点在坐标原点O,始边
顶点在坐标原点O,始边 轴的非负半轴重合,点P在
轴的非负半轴重合,点P在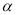 的终边上,点
的终边上,点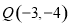 ,且
,且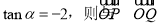 夹角的余弦值为( )
夹角的余弦值为( )
A.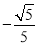 B.
B.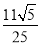 C.
C.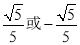 D.
D.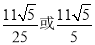
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省日照市高三3月第一次模拟考试理科数学试卷(解析版) 题型:解答题
已知函数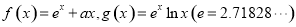 ..
..
(1)设曲线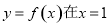 处的切线为
处的切线为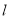 ,点(1,0)到直线l的距离为
,点(1,0)到直线l的距离为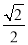 ,求a的值;
,求a的值;
(2)若对于任意实数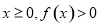 恒成立,试确定
恒成立,试确定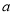 的取值范围;
的取值范围;
(3)当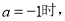 是否存在实数
是否存在实数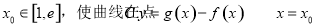 处的切线与y轴垂直?若存在,求出
处的切线与y轴垂直?若存在,求出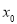 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省日照市高三3月第一次模拟考试文科数学试卷(解析版) 题型:选择题
已知函数① ②
②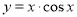 ,③
,③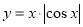 ,④
,④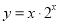 的部分图象如下,但顺序被打乱,则按照图象从左到右的顺序,对应的函数序号正确的一组是( )
的部分图象如下,但顺序被打乱,则按照图象从左到右的顺序,对应的函数序号正确的一组是( )
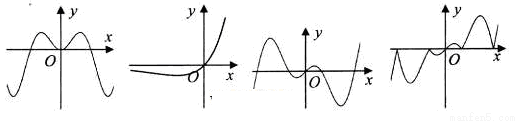
A.①④②③ B.①④③② C.④①②③ D.③④②①
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省东营市高三4月统一质量检测考试理科数学试卷(解析版) 题型:解答题
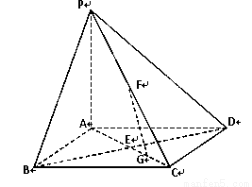
如图,在底面是正方形的四棱锥P—ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
(1)求证:BD⊥FG;
(2)确定点G在线段AC上的位置,使FG//平面PBD,并说明理由.
(3)当二面角B—PC—D的大小为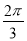 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com