
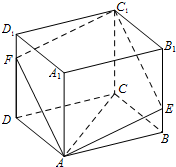
 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,E,F分别在棱BB1,DD1上,且AF∥EC1.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,E,F分别在棱BB1,DD1上,且AF∥EC1. 的正方形,且BE=1,DF=2,求线段CC1的长,并证明:AC⊥EC1.
的正方形,且BE=1,DF=2,求线段CC1的长,并证明:AC⊥EC1.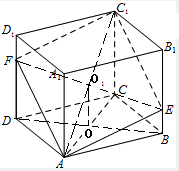
 C1C=
C1C= (BE+EF).
(BE+EF).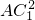 -
-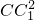 =2AE2-
=2AE2-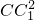 =12-9=3,AB2=AE2-BE2=6-1=5
=12-9=3,AB2=AE2-BE2=6-1=5

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
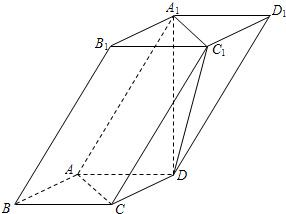 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.查看答案和解析>>
科目:高中数学 来源: 题型:
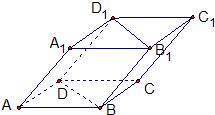 如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底面边长均为2a,且∠A1AD=∠A1AB=60°,则侧棱AA1和截面B1D1DB的距离是
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底面边长均为2a,且∠A1AD=∠A1AB=60°,则侧棱AA1和截面B1D1DB的距离是查看答案和解析>>
科目:高中数学 来源: 题型:
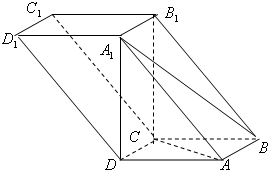 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱A1A=2,
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱A1A=2,| AP |
| PA1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.
(2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•天津)如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,
(2013•天津)如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,
| ||
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com