
【题目】已知锐角三角形![]() 的外接圆半径是
的外接圆半径是![]() ,点
,点![]() ,
,![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() ,
,![]() 上。求证:
上。求证:![]() ,
,![]() ,
,![]() 是
是![]() 的三条高的充要条件是
的三条高的充要条件是![]() ,式中
,式中![]() 是
是![]() 的面积。
的面积。
【答案】见解析
【解析】
△ABC的外接圆的圆心为O, ![]() ,连接
,连接![]() ,
, ![]() .
.
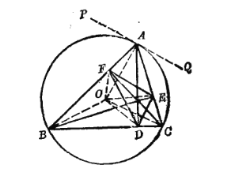
证法一:必要性因△ABC为锐角三角形,故点O在△ABC内.于是, ![]()
过点A作⊙O的切线PQ,则![]() .
.
又B,C,E,F四点共圆,
∴![]()
于是, ![]()
PQ∥E, ![]() .
.
![]() .
.
同理, ![]()
![]() .
.
从而, ![]()
充分性,设![]()
先证![]() .用反证法.若OA与EF不垂直,则
.用反证法.若OA与EF不垂直,则![]() .
.
又![]() ,
,
![]() .
.
所以, ![]() .
.
这和已知条件矛盾.故![]()
同理![]()
过点A作⊙O的切线PQ,则![]()
∵![]() ,∴PQ∥EF,
,∴PQ∥EF,![]() ,
,
因此,B,C,E,F四点共圆,
同理A,B,D,E四点共圆,C,A,F,D四点共圆,
故![]() ,
,![]() ,
,
于是, ![]() .
.
又![]() 四点共圆,
四点共圆,
![]() ,
,
∴![]()
![]() ,
,
即![]() .
.
证法二:因![]() 为锐角三角形,故
为锐角三角形,故
点![]() 在
在![]() 内.
内.
∴![]()
![]()
![]()
![]() .
.
因![]() 四点共圆,故:
四点共圆,故:
∴![]() .
.
∴![]() ,
,
![]() .
.
即![]() .
.
同理![]() .
.
从而![]()
设![]() 是
是![]() 的三条高,由证法一知,
的三条高,由证法一知,![]() ,
,
![]() .
.
又设点D,E,F分别在边BC;CA,AB上,使![]()
由证法一知,![]() ,
,![]() ,
,
∴![]()
若点F与F不重合,不妨设![]() ,
,
则![]() .
.
又![]() .
.
从而![]() ,矛盾.于是点F与
,矛盾.于是点F与![]() 重合.
重合.
同理,点E与E重合,点D与![]() 重合.
重合.
故AD,BE,CF是△ABC的三条高


科目:高中数学 来源: 题型:
【题目】某学习小组由学生和教师组成,人员构成同时满足以下三个条件:①男生人数多于女生人数;②女生人数多于教师人数;③教师人数的两倍多于男生人数.问:
(1)若教师人数为4,则女生人数的最大值为多少?
(2)该小组人数的最小值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,圆
,圆![]() .
.
(1)若直线![]() 过点
过点![]() 且到圆心
且到圆心![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点(
两点(![]() 的斜率为负),当
的斜率为负),当![]() 时,求以线段
时,求以线段![]() 为直径的圆的方程.
为直径的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,纵、横坐标都是整数的点称为整点。请设计一种方法将所有的整点染色,每一个整点染成白色、红色或黑色中的一种颜色,使得
(1)每一种颜色的点出现在无穷多条平行于横轴的直线上;
(2)对于任意白点![]() 、红点
、红点![]() 及黑点
及黑点![]() ,总可以找到一个红点
,总可以找到一个红点![]() ,使
,使![]() 为一平行四边形。证明你设计的方法符合上述要求。
为一平行四边形。证明你设计的方法符合上述要求。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,DA=DC=2,![]() ,E是C1D1的中点,F是CE的中点.
,E是C1D1的中点,F是CE的中点.
(1)求证:EA∥平面BDF;
(2)求证:平面BDF⊥平面BCE;
(3)求二面角D﹣EB﹣C的正切值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com