
【题目】已知![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 上一点
上一点![]() 到焦点
到焦点![]() 的距离为
的距离为![]() ,若点
,若点![]() 为抛物线
为抛物线![]() 准线上的动点,给出以下命题:
准线上的动点,给出以下命题:
①当![]() 为正三角形时,
为正三角形时,![]() 的值为
的值为![]() ;
;
②存在![]() 点,使得
点,使得![]() ;
;
③若![]() ,则
,则![]() 等于
等于![]() ;
;
④![]() 的最小值为
的最小值为![]() ,则
,则![]() 等于
等于![]() 或
或![]() .
.
其中正确的是( )
A.①③④B.②③C.①③D.②③④
【答案】A
【解析】
对于①可知,当![]() 为正三角形时
为正三角形时![]() 与准线垂直,画出图形结合几何关系即可求得
与准线垂直,画出图形结合几何关系即可求得![]() 的值;对于②根据向量关系可知
的值;对于②根据向量关系可知![]() ,结合点的位置即可判断;对于③,作出几何图形,根据线段比例关系即可求得
,结合点的位置即可判断;对于③,作出几何图形,根据线段比例关系即可求得![]() 的值;对于④,作
的值;对于④,作![]() 关于准线的对称点
关于准线的对称点![]() ,连接
,连接![]() 交准线于
交准线于![]() ,可知
,可知![]() 即为
即为![]() 的最小值,根据线段几何关系及最小值即可求得
的最小值,根据线段几何关系及最小值即可求得![]() 的值.
的值.
对于①,当![]() 为正三角形时,如下图所示,
为正三角形时,如下图所示,
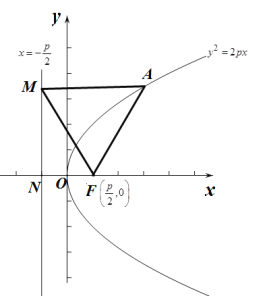
抛物线的准线交![]() 轴于
轴于![]() ,
,
![]() ,由抛物线定义可知
,由抛物线定义可知![]() ,则
,则![]() 与准线垂直,
与准线垂直,
所以![]() ,
,
则![]() ,所以
,所以![]() ,
,
而![]() ,即
,即![]() ,所以①正确;
,所以①正确;
对于②,假设存在![]() 点,使得
点,使得![]() ,即
,即![]() ,
,
所以![]() 点为
点为![]() 的中点,
的中点,
由抛物线图像与性质可知,![]() 为抛物线上一点,
为抛物线上一点,![]() 为焦点,线段
为焦点,线段![]() 在
在![]() 轴右侧,
轴右侧,
点![]() 在抛物线
在抛物线![]() 准线上,在
准线上,在![]() 轴左侧,因而
轴左侧,因而![]() 不可能为
不可能为![]() 的中点,所以②错误;
的中点,所以②错误;
对于③,若![]() ,则
,则![]() ,作
,作![]() 垂直于准线并交于
垂直于准线并交于![]() ,准线交
,准线交![]() 轴于
轴于![]() ,如下图所示:
,如下图所示:
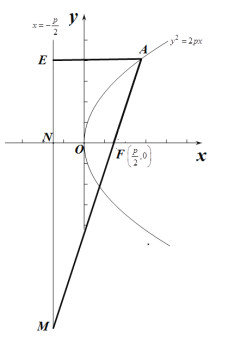
由抛物线定义可知![]() ,
,
根据相似三角形中对应线段成比例可知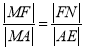 ,即
,即![]() ,
,
解得![]() ,所以③正确;
,所以③正确;
对于④,作![]() 关于准线的对称点
关于准线的对称点![]() ,连接
,连接![]() 交准线于
交准线于![]() ,作
,作![]() 垂直于准线并交于
垂直于准线并交于![]() ,作
,作![]() 垂直于
垂直于![]() 轴并交于
轴并交于![]() ,如下图所示:
,如下图所示:
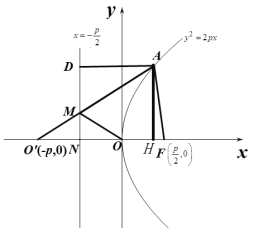
根据对称性可知,此时![]() 即为
即为![]() 的最小值,
的最小值,
由抛物线定义可知![]() ,所以
,所以![]() 的横坐标为
的横坐标为![]() ,
,
代入抛物线可知![]() ,
,
![]() 的最小值为
的最小值为![]() ,
,![]() ,
,
则![]() ,即
,即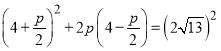 ,
,
化简可得![]() ,即
,即![]() ,
,
解得![]() 或
或![]() ,所以④正确;
,所以④正确;
综上所述,正确的为①③④.
故选:A.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() ,以原点
,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .若将曲线
.若将曲线![]() 上的所有点的横坐标缩小到原来的一半,纵坐标伸长到原来的
上的所有点的横坐标缩小到原来的一半,纵坐标伸长到原来的![]() 倍,得曲线
倍,得曲线![]() .
.
(1)写出直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() , 直线
, 直线![]() 与曲线
与曲线![]() 的两个交点分别为
的两个交点分别为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学参加某个知识答题游戏节目,答题分两轮,第一轮为“选题答题环节”第二轮为“轮流坐庄答题环节”.首先进行第一轮“选题答题环节”,答题规则是:每位同学各自从备选的5道不同题中随机抽出3道题进行答题,答对一题加10分,答错一题(不答视为答错)减5分,已知甲能答对备选5道题中的每道题的概率都是![]() ,乙恰能答对备选5道题中的其中3道题;第一轮答题完毕后进行第二轮“轮流坐庄答题环节”,答题规则是:先确定一人坐庄答题,若答对,继续答下一题…,直到答错,则换人(换庄)答下一题…以此类推.例如若甲首先坐庄,则他答第1题,若答对继续答第2题,如果第2题也答对,继续答第3题,直到他答错则换成乙坐庄开始答下一题,…直到乙答错再换成甲坐庄答题,依次类推两人共计答完20道题游戏结束,假设由第一轮答题得分期望高的同学在第二轮环节中最先开始作答,且记第
,乙恰能答对备选5道题中的其中3道题;第一轮答题完毕后进行第二轮“轮流坐庄答题环节”,答题规则是:先确定一人坐庄答题,若答对,继续答下一题…,直到答错,则换人(换庄)答下一题…以此类推.例如若甲首先坐庄,则他答第1题,若答对继续答第2题,如果第2题也答对,继续答第3题,直到他答错则换成乙坐庄开始答下一题,…直到乙答错再换成甲坐庄答题,依次类推两人共计答完20道题游戏结束,假设由第一轮答题得分期望高的同学在第二轮环节中最先开始作答,且记第![]() 道题也由该同学(最先答题的同学)作答的概率为
道题也由该同学(最先答题的同学)作答的概率为![]() (
(![]() ),其中
),其中![]() ,已知供甲乙回答的20道题中,甲,乙两人答对其中每道题的概率都是
,已知供甲乙回答的20道题中,甲,乙两人答对其中每道题的概率都是![]() ,如果某位同学有机会答第
,如果某位同学有机会答第![]() 道题且回答正确则该同学加10分,答错(不答视为答错)则减5分,甲乙答题相互独立;两轮答题完毕总得分高者胜出.回答下列问题
道题且回答正确则该同学加10分,答错(不答视为答错)则减5分,甲乙答题相互独立;两轮答题完毕总得分高者胜出.回答下列问题
(1)请预测第二轮最先开始作答的是谁?并说明理由
(2)①求第二轮答题中![]() ,
,![]() ;
;
②求证![]() 为等比数列,并求
为等比数列,并求![]() (
(![]() )的表达式.
)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高中三个年级共有4000人,为了了解各年级学周末在家的学习情况,现通过分层抽样的方法获得相关数据如下(单位:小时),其中高一学生周末的平均学习时间记为![]() .
.
高一:14 15 15.5 16.5 17 17 18 19
高二:15 16 16 16 17 17 18.5
高三:16 17 18 21.5 24
(1)求每个年级的学生人数;
(2)从高三被抽查的同学中随机抽取2人,求2人学习时间均超过![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现从某学校中选出![]() 名学生,统计了
名学生,统计了![]() 名学生一周的户外运动时间(分钟)总和,得到如图所示的频率分布直方图和统计表格.
名学生一周的户外运动时间(分钟)总和,得到如图所示的频率分布直方图和统计表格.

(1)写出![]() 的值,并估计该学校人均每周的户外运动时间(同一组数据用该组区间的中点值作代表);
的值,并估计该学校人均每周的户外运动时间(同一组数据用该组区间的中点值作代表);
(2)假设![]() ,则户外运动时长为
,则户外运动时长为![]() 的学生中,男生人数比女生人数多的概率.
的学生中,男生人数比女生人数多的概率.
(3)若![]() ,完成下列
,完成下列![]() 列联表,并回答能否有90%的把握认为“每周至少运动130分钟与性别有关”?
列联表,并回答能否有90%的把握认为“每周至少运动130分钟与性别有关”?
每周户外运动时间不少于130分钟 | 每周户外运动时间少于130分钟 | 合计 | |
男 | |||
女 | |||
合计 |
附: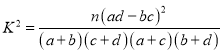 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左,右焦点,
的左,右焦点,![]() 两点分别是椭圆
两点分别是椭圆![]() 的上,下顶点,
的上,下顶点,![]() 是等腰直角三角形,延长
是等腰直角三角形,延长![]() 交椭圆
交椭圆![]() 于
于![]() 点,且
点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的动点,直线
的动点,直线![]() 与直
与直![]() 分别相交于
分别相交于![]() 两点,点
两点,点![]() ,求证:
,求证:![]() 的外接圆恒过原点
的外接圆恒过原点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为实数,用
为实数,用![]() 表示不超过
表示不超过![]() 的最大整数,例如
的最大整数,例如![]() ,
,![]() ,
,![]() ,对于函数
,对于函数![]() ,若存在
,若存在![]() ,
,![]() ,使得
,使得![]() ,则称函数
,则称函数![]() 是“
是“![]() 函数”.
函数”.
(1)判断函数![]() ,
,![]() 是否是“
是否是“![]() 函数”;
函数”;
(2)设函数![]() 是定义在
是定义在![]() 上的周期函数,其最小正周期是
上的周期函数,其最小正周期是![]() ,若
,若![]() 不是“
不是“![]() 函数”,求
函数”,求![]() 的最小值;
的最小值;
(3)若函数![]() 是“
是“![]() 函数”,求
函数”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了比较两种治疗失眠症的药(分别称为![]() 药,
药,![]() 药)的疗效,某机构随机地选取
药)的疗效,某机构随机地选取![]() 位患者服用
位患者服用![]() 药,
药,![]() 位患者服用
位患者服用![]() 药,观察这
药,观察这![]() 位患者的睡眠改善情况.这些患者服用一段时间后,根据患者的日平均增加睡眠时间(单位:
位患者的睡眠改善情况.这些患者服用一段时间后,根据患者的日平均增加睡眠时间(单位:![]() ),以整数部分当茎,小数部分当叶,绘制了如下茎叶图:
),以整数部分当茎,小数部分当叶,绘制了如下茎叶图:
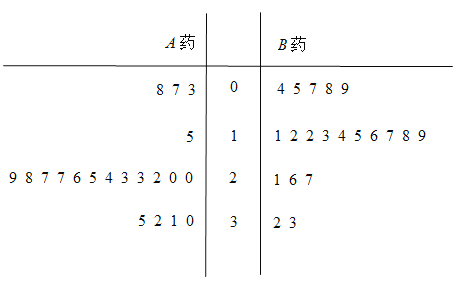
(1)根据茎叶图判断哪种药对增加睡眠时间更有效?并说明理由;
(2)求这![]() 名患者日平均增加睡眠时间的中位数
名患者日平均增加睡眠时间的中位数![]() ,并将日平均增加睡眠时间超过
,并将日平均增加睡眠时间超过![]() 和不超过
和不超过![]() 的患者人数填入下面的列联表:
的患者人数填入下面的列联表:
超过 | 不超过 | |
服用 | ||
服用 |
(3)根据(2)中的列联表,能否有![]() 的把握认为
的把握认为![]() 两种药的疗效有差异?
两种药的疗效有差异?
附: 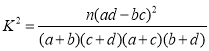 .
.
| 0.01 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com