
设 的定义域为
的定义域为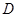 ,若
,若 满足下面两个条件,则称
满足下面两个条件,则称 为闭函数.
为闭函数.
① 在
在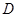 内是单调函数;②存在
内是单调函数;②存在 ,使
,使 在
在 上的值域为
上的值域为 ,
,
如果 为闭函数,那么
为闭函数,那么 的取值范围是( )
的取值范围是( )
A. ≤ ≤ | B. ≤ ≤ <1 <1 | C. | D. <1 <1 |
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com