
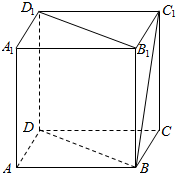
 如图,正方体ABCD-A1B1C1D1中,直线BC1和B1D1所成角的大小为60°;直线BC1和平面B1D1DB所成角的大小为30°.
如图,正方体ABCD-A1B1C1D1中,直线BC1和B1D1所成角的大小为60°;直线BC1和平面B1D1DB所成角的大小为30°. 分析 连结DC1,A1C1,设A1C1∩B1D1=O,连结BO,由B1D1∥BD,得∠DBC1是线BC1和B1D1所成角,由此能求出直线BC1和B1D1所成角的大小;推导出C1O⊥平面B1D1DB,从而∠OBC1是直线BC1和平面B1D1DB所成角,由此能求出直线BC1和平面B1D1DB所成角的大小.
解答 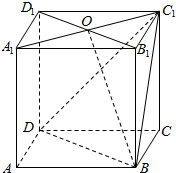 解:连结DC1,A1C1,设A1C1∩B1D1=O,连结BO,
解:连结DC1,A1C1,设A1C1∩B1D1=O,连结BO,
∵B1D1∥BD,∴∠DBC1是线BC1和B1D1所成角,
∵BD=BC1=DC1,
∴∠DBC1=60°,
∴直线BC1和B1D1所成角的大小为60°;
正方体ABCD-A1B1C1D1中,
∵B1D1⊥A1C1,BB1⊥A1C1,B1D1∩BB1=B1,
∴C1O⊥平面B1D1DB,
∴∠OBC1是直线BC1和平面B1D1DB所成角,
∵$O{C}_{1}=\frac{1}{2}B{C}_{1}$,∴$sin∠OB{C}_{1}=\frac{O{C}_{1}}{B{C}_{1}}$=$\frac{1}{2}$,
∴∠OBC1=30°.
∴直线BC1和平面B1D1DB所成角为30°.
故答案为:60°,30°.
点评 本题考查直线与平面所成角的大小的求法,考查线面角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | PM2.5浓度 | 日期 | PM2.5浓度 | 日期 | PM2.5浓度 |
| 11-1 | 137 | 11-11 | 144 | 11-21 | 40 |
| 11-2 | 143 | 11-12 | 166 | 11-22 | 42 |
| 11-3 | 145 | 11-13 | 197 | 11-23 | 35 |
| 11-4 | 193 | 11-14 | 194 | 11-24 | 53 |
| 11-5 | 133 | 11-15 | 219 | 11-25 | 88 |
| 11-6 | 22 | 11-16 | 41 | 11-26 | 29 |
| 11-7 | 22 | 11-17 | 90 | 11-27 | 199 |
| 11-8 | 57 | 11-18 | 46 | 11-28 | 287 |
| 11-9 | 111 | 11-19 | 80 | 11-29 | 291 |
| 11-10 | 134 | 11-20 | 67 | 11-30 | 452 |
| 空气质量指数类别 | PM2.5 24小时浓度均值 | 频数 | 频率 |
| 优 | 0-35 | 4 | $\frac{2}{15}$ |
| 良 | 36-75 | 7 | $\frac{7}{30}$ |
| 轻度污染 | 76-115 | 4 | |
| 中度污染 | 116-150 | 6 | |
| 重度污染 | 151-250 | ||
| 严重污染 | 251-500 | ||
| 合计 | / | 30 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
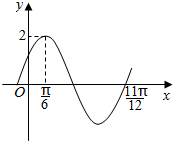 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,丨φ丨<$\frac{π}{2}$)的部分图象如图所示,则f(x)的解析式为( )
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,丨φ丨<$\frac{π}{2}$)的部分图象如图所示,则f(x)的解析式为( )| A. | f(x)=2sin(x+$\frac{π}{3}$) | B. | f(x)=2sin(2x+$\frac{π}{6}$) | C. | f(x)=2sin(2x-$\frac{π}{6}$) | D. | f(x)=2sin(4x-$\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | ±$\frac{1}{2}$ | D. | ±2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com