
【题目】设函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 存在两个零点
存在两个零点![]() .
.
①实数![]() 的取值范围;
的取值范围;
②证明:![]() .
.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②详见解析.
;②详见解析.
【解析】
(1)求得![]() 的导数,可得切线的斜率,由点斜式方程可得切线方程;
的导数,可得切线的斜率,由点斜式方程可得切线方程;
(2)①求得![]() 的导数,讨论
的导数,讨论![]() 的符号,求得单调性,结合函数的零点,可得最小值小于
的符号,求得单调性,结合函数的零点,可得最小值小于![]() ,解不等式可得
,解不等式可得![]() 的范围;
的范围;
②由题意可得![]() ,作差可得
,作差可得![]() ,运用分析法证明,转化为证明
,运用分析法证明,转化为证明![]() ,设
,设![]() ,可得
,可得![]() ,设
,设![]() ,求得导数,判断单调性,即可得证.
,求得导数,判断单调性,即可得证.
(1)函数![]() 的导函数为
的导函数为![]() ,
,
可得![]() 在
在![]() 处切线的斜率为
处切线的斜率为![]() ,
,
则切线方程为![]() ,即
,即![]() .
.
(2)
①函数![]() 的导函数为
的导函数为![]() ,
,
若![]() ,则
,则![]() 在
在![]() 上递增,不成立;
上递增,不成立;
当![]() 时,
时,![]() 在
在![]() 时递增,在
时递增,在![]() 时递减,
时递减,
所以![]() 在
在![]() 处取得极小值,且为最小值
处取得极小值,且为最小值![]() ,
,
由题意可得![]() ,解得
,解得![]() .
.
②依题意可得![]() ,
,
两式相减并化简得![]() ,要证
,要证![]() ,
,
即证![]() ,
,
即为![]() ,即为
,即为![]() ,即为
,即为![]() ,
,
由![]() 可得
可得![]() ,设
,设![]() ,
,
可得![]() ,
,
设![]() ,
,
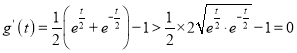 ,
,
则![]() 在
在![]() 递增,而
递增,而![]() ,所以
,所以![]() ,
,
所以![]() ,
,
则![]() .
.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:
【题目】随着经济全球化、信息化的发展,企业之间的竞争从资源的争夺转向人才的竞争,吸引、留住培养和用好人才成为人力资源管理的战略目标和紧迫任务,在此背景下,某信息网站在15个城市中对刚毕业的大学生的月平均收入薪资和月平均期望薪资做了调查,数据如下图所示.
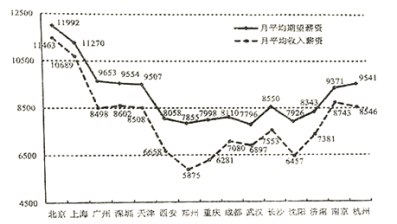
(Ⅰ)若某大学毕业生从这15座城市中随机选择一座城市就业,求该生选中月平均收入薪资高于8500元的城市的概率;
(Ⅱ)若从月平均收入薪资与月平均期望薪资之差高于1100元的城市中随机选择2座城市,求这2座城市的月平均期望薪资都低于8500元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】推进垃圾分类处理,是落实绿色发展理念的必然选择,也是打赢污染防治攻坚战的重要环节.为了解居民对垃圾分类的了解程度,某社区居委会随机抽取1000名社区居民参与问卷测试,并将问卷得分绘制频率分布表如下:
得分 |
|
|
|
|
|
|
|
男性人数 | 40 | 90 | 120 | 130 | 110 | 60 | 30 |
女性人数 | 20 | 50 | 80 | 110 | 100 | 40 | 20 |
(1)从该社区随机抽取一名居民参与问卷测试,试估计其得分不低于60分的概率;
(2)将居民对垃圾分类的了解程度分为“比较了解“(得分不低于60分)和“不太了解”(得分低于60分)两类,完成![]() 列联表,并判断是否有95%的把握认为“居民对垃圾分类的了解程度”与“性别”有关?
列联表,并判断是否有95%的把握认为“居民对垃圾分类的了解程度”与“性别”有关?
不太了解 | 比较了解 | |
男性 | ||
女性 |
(3)从参与问卷测试且得分不低于80分的居民中,按照性别进行分层抽样,共抽取10人,连同![]() 名男性调查员一起组成3个环保宜传队.若从这
名男性调查员一起组成3个环保宜传队.若从这![]() 中随机抽取3人作为队长,且男性队长人数占的期望不小于2.求
中随机抽取3人作为队长,且男性队长人数占的期望不小于2.求![]() 的最小值.
的最小值.
附:![]()
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰梯形![]() 中,两腰
中,两腰![]() ,底边
,底边![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的三等分点,
的三等分点,![]() 是
是![]() 的中点.分别沿
的中点.分别沿![]() ,
,![]() 将四边形
将四边形![]() 和
和![]() 折起,使
折起,使![]() ,
,![]() 重合于点
重合于点![]() ,得到如图2所示的几何体.在图2中,
,得到如图2所示的几何体.在图2中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
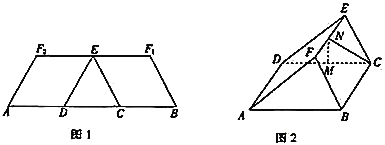
(1)证明:![]() 平面
平面![]() .
.
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知单调递增的等比数列![]() 满足:
满足:![]() .且
.且![]() 是
是![]() ,
,![]() 的等差中项.又数列
的等差中项.又数列![]() 满足:
满足:![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,且数列
,且数列![]() 为等比数列,求
为等比数列,求![]() 的值;
的值;
(3)若![]() ,且
,且![]() 为数列
为数列![]() 的最小项,求
的最小项,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有3名医生,5名护士、2名麻醉师.
(1)从中选派1名去参加外出学习,有多少种不同的选法?
(2)从这些人中选出1名医生、1名护士和1名麻醉师组成1个医疗小组,有多少种不同的选法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名同学参加一项射击比赛游戏,其中任何一人每射击一次击中目标得2分,未击中目标得0分.若甲、乙两人射击的命中率分别为![]() 和
和![]() ,且甲、乙两人各射击一次得分之和为2的概率为
,且甲、乙两人各射击一次得分之和为2的概率为![]() .假设甲、乙两人射击互不影响,则
.假设甲、乙两人射击互不影响,则![]() 值为( )
值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级三个班共有学生120名,这三个班的男女生人数如下表所示,已知在全年级中随机抽取1名学生,抽到二班女生的概率是0.2,则![]() _________.现用分层抽样的方法在全年级抽取30名学生,则应在三班抽取的学生人数为________.
_________.现用分层抽样的方法在全年级抽取30名学生,则应在三班抽取的学生人数为________.
一班 | 二班 | 三班 | |
女生人数 | 20 |
|
|
男生人数 | 20 | 20 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx﹣x+1,g(x)=ex﹣ax,a∈R.
(Ⅰ)求f(x)的最小值;
(Ⅱ)若g(x)≥1在R上恒成立,求a的值;
(Ⅲ)求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com