
【题目】求由直线x=1、x=2、y=0及曲线![]() 围成的图形的面积S.
围成的图形的面积S.
【答案】详见解析
【解析】(1)分割:
在区间[1,2]上等间隔地插入n-1个点,将它等分成n个小区间:
![]() ,则第i个区间为
,则第i个区间为![]() (i=1,2,…,n),其长度为Δx=
(i=1,2,…,n),其长度为Δx=![]() ,
,
分别过上述n-1个分点作x轴的垂线,把曲边梯形分成n个小曲边梯形(如图),它们的面积记作:ΔS1,ΔS2,…,ΔSn,则小曲边梯形面积的和为S=![]() .
.

(2)近似代替:
记f(x)=![]() .当n很大,即Δx很小时,在区间
.当n很大,即Δx很小时,在区间![]() 上,可以认为f(x)=
上,可以认为f(x)=![]() 的值变化很小,近似地等于一个常数,不妨认为它等于
的值变化很小,近似地等于一个常数,不妨认为它等于 .从图形上看,就是用平行于x轴的直线段近似地代替小曲边梯形的曲边.这样,在区间
.从图形上看,就是用平行于x轴的直线段近似地代替小曲边梯形的曲边.这样,在区间![]() 上,用小矩形面积ΔSi′近似地代替ΔSi,即在局部小范围内“以直代曲”,则有ΔSi≈ΔSi′=
上,用小矩形面积ΔSi′近似地代替ΔSi,即在局部小范围内“以直代曲”,则有ΔSi≈ΔSi′= Δx=
Δx=![]() =
=![]() (i=1,2,…,n).
(i=1,2,…,n).
(3)求和:
小曲边梯形的面积和Sn=![]() Si≈
Si≈![]() Si′=
Si′=![]() =
=
![]()
=![]()
=![]()
![]() .从而得到S的近似值S≈Sn=
.从而得到S的近似值S≈Sn=![]() .
.
(4)取极限:
分别将区间[1,2]等分成8,16,20,…等份时,Sn越来越趋向于S,
从而有S=![]() Sn=
Sn=![]() .
.
∴由直线x=1,x=2,y=0及曲线y=![]() 围成的图形的面积S为
围成的图形的面积S为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 两个小岛相距
两个小岛相距![]() 海里,
海里,![]() 岛在
岛在![]() 岛的正南方,现在甲船从
岛的正南方,现在甲船从![]() 岛出发,以
岛出发,以![]() 海里/时的速度向
海里/时的速度向![]() 岛行驶,而乙船同时以
岛行驶,而乙船同时以![]() 海里/时的速度离开
海里/时的速度离开![]() 岛向南偏东
岛向南偏东![]() 方向行驶,行驶多少时间后,两船相距最近?并求出两船的最近距离.
方向行驶,行驶多少时间后,两船相距最近?并求出两船的最近距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 是单调递增函数,求实数
是单调递增函数,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 内有两个实数根
内有两个实数根![]() ,记
,记![]() ,求实数
,求实数![]() 的取值范围 .
的取值范围 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在△ABC中,a=b·cos C+c·cos B,其中a,b,c分别为角A,B,C的对边,在四面体PABC中,S1,S2,S3,S分别表示△PAB,△PBC,△PCA,△ABC的面积,α,β,γ依次表示面PAB,面PBC,面PCA与底面ABC所成二面角的大小.写出对四面体性质的猜想,并证明你的结论


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体,它的下面是一个圆柱,上面是一个圆锥,并且圆锥的底面与圆柱的上底面重合,圆柱的底面直径为3 cm,高为4 cm,圆锥的高为3 cm,画出此几何体的直观图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知任意角
中,已知任意角![]() 以坐标原点
以坐标原点![]() 为顶点,
为顶点,![]() 轴的非负半轴为始边,若终边经过点
轴的非负半轴为始边,若终边经过点![]() ,且
,且![]() ,定义:
,定义:![]() ,称“
,称“![]() ”为“正余弦函数”,对于“正余弦函数
”为“正余弦函数”,对于“正余弦函数![]() ”,有同学得到以下性质:
”,有同学得到以下性质:
①该函数的值域为![]() ; ②该函数的图象关于原点对称;
; ②该函数的图象关于原点对称;
③该函数的图象关于直线![]() 对称; ④该函数为周期函数,且最小正周期为
对称; ④该函数为周期函数,且最小正周期为![]() ;
;
⑤该函数的递增区间为![]() .
.
其中正确的是__________.(填上所有正确性质的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表。
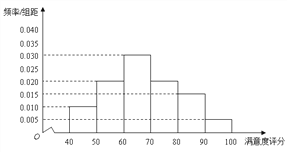
A地区用户满意度评分的频率分布直方图

B地区用户满意度评分的频数分布表
(Ⅰ)在答题卡上作出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);
(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
估计哪个地区的满意度等级为不满意的概率大?说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com