
【题目】如图所示的多面体ABCDEF满足:正方形ABCD与正三角形FBC所在的两个平面互相垂直,FB∥AE且FB=2EA.

(1)证明:平面EFD⊥平面ABFE;
(2)若AB=2,求多面体ABCDEF的体积.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由已知求解三角形可得![]() ,由面面垂直的性质可得
,由面面垂直的性质可得![]() 平面
平面![]() ,证明平面
,证明平面![]() 平面
平面![]() ,则
,则![]() 平面
平面![]() ,得到
,得到![]() .再由线面垂直的判定可得
.再由线面垂直的判定可得![]() 平面
平面![]() ,从而得到平面
,从而得到平面![]() 平面
平面![]() ;
;
(2)连接![]() ,则多面体
,则多面体![]() 分为四棱锥
分为四棱锥![]() 和三棱锥
和三棱锥![]() .分别求出四棱锥
.分别求出四棱锥![]() 与
与![]() 的体积,则多面体
的体积,则多面体![]() 的体积可求.
的体积可求.
(1)证明:由题意可得,四边形ABCD是正方形且三角形FBC是正三角形,
∴BC∥AD,BC=AD,FB=BC,∠FBC=60°,
又∵FB∥AE且FB=2EA,
∴∠EAD=60°,
在△EAD中,设EA=a,则AD=2a,又∠EAD=60°,
由余弦定理得:![]() .
.
∵DE2+AE2=AD2,
∴ED⊥AE,
∵平面ABCD⊥平面FBC,AB⊥BC,平面ABCD∩平面FBC=BC,且AB平面ABCD,
∴AB⊥平面BCF,
∵BC∥AD,EA∥FB,FB∩BC=B,且FB,BC平面FBC,
EA,AD平面EAD,
∴平面EAD∥平面FBC,则AB⊥平面EAD.
又∵ED平面EAD,
∴AB⊥ED.
综上,ED⊥AE,ED⊥AB,EA∩AB=A,且EA,AB平面ABEF,
∴DE⊥平面ABEF,
又∵DE平面DEF,
∴平面EFD⊥平面ABFE;
(2)连接BD,
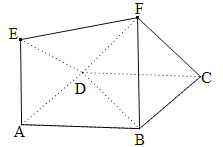
则多面体ABCDEF分为四棱锥D﹣ABFE和三棱锥D﹣BCF.
由(1)可得,ED⊥平面ABFE,
∴![]() .
.
由(1)可得AB⊥平面BCF,又CD∥AB,
∴CD⊥平面BCF,
∴![]() .
.
综上,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() ,
,![]() 为参数
为参数![]() ,在以坐标原点为极点,x轴非负半轴为极轴的极坐标系中,曲线
,在以坐标原点为极点,x轴非负半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
![]() Ⅰ
Ⅰ![]() 写出
写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
![]() Ⅱ
Ⅱ![]() 若
若![]() 与
与![]() 相交于A,B两点,求
相交于A,B两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+|x+2|.
(1)若a=1.解不等式f(x)≤x2﹣1;
(2)若a>0,b>0,c>0.且f(x)的最小值为4﹣b﹣c.求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
某投资公司在2010年年初准备将1000万元投资到“低碳”项目上,现有两个项目供选择:
项目一:新能源汽车.据市场调研,投资到该项目上,到年底可能获利![]() ,也可能亏损
,也可能亏损![]() ,且这两种情况发生的概率分别为
,且这两种情况发生的概率分别为![]() 和
和![]() ;
;
项目二:通信设备.据市场调研,投资到该项目上,到年底可能获利![]() ,可能亏损
,可能亏损![]() ,也可能不赔不赚,且这三种情况发生的概率分别为
,也可能不赔不赚,且这三种情况发生的概率分别为![]() 、
、![]() 和
和![]()
(Ⅰ)针对以上两个投资项目,请你为投资公司选择一个合理的项目,并说明理由;
(Ⅱ)若市场预期不变,该投资公司按照你选择的项目长期投资(每一年的利润和本金继续用作投资),问大约在哪一年的年底总资产(利润+本金)可以翻一番?
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为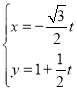 ,(t为参数)以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2
,(t为参数)以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2![]() sinθ,
sinθ,
(1)求直线l的普通方程及曲线C的直角坐标方程;
(2)直线l与x轴交于点P,与曲线C交于A,B两点,求|PA|+|PB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com